题目内容
1. 如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )
如图,经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),则0<kx+b<4x+4的解集为( )| A. | x<$\frac{1}{3}$ | B. | -$\frac{1}{3}$<x<1 | C. | x<1 | D. | -1<x<1 |
分析 将点A(m,$\frac{8}{3}$)代入y=4x+4求出m的值,观察直线y=kx+b落在直线y=4x+4的下方且直线y=kx+b落在x轴上方的部分对应的x的取值即为所求.
解答 解:∵经过点B(1,0)的直线y=kx+b与直线y=4x+4相交于点A(m,$\frac{8}{3}$),
∴4m+4=$\frac{8}{3}$,
∴m=-$\frac{1}{3}$,
∴直线y=kx+b与直线y=4x+4的交点A的坐标为(-$\frac{1}{3}$,$\frac{8}{3}$),直线y=kx+b与x轴的交点坐标为B(1,0),
又∵当x<1时,kx+b>0,
当x>-$\frac{1}{3}$时,kx+b<4x+4,
∴0<kx+b<4x+4的解集为-$\frac{1}{3}$<x<1.
故选B.
点评 本题考查了一次函数与一元一次不等式的关系:从函数的角度看,就是寻求使一次函数y=ax+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.方程x2-2x=0的解为( )
| A. | x=2 | B. | x=0 | C. | x1=0 或 x2=2 | D. | x1=0 或 x2=-2 |
16. 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
 如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )
如图,某厂生产一种扇形折扇,OB=10cm,AB=20cm,其中裱花的部分是用纸糊的,若扇子完全打开摊平时纸面面积为$\frac{1000}{3}$π cm2,则扇形圆心角的度数为( )| A. | 120° | B. | 140° | C. | 150° | D. | 160° |

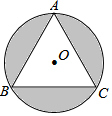 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$. 如图,在平面直角坐标系中.O为坐标原点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A,B两点.点P从点A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.过点P与直线AB垂直的直线与y轴交于点E.
如图,在平面直角坐标系中.O为坐标原点,直线y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A,B两点.点P从点A出发,以每秒1个单位的速度沿射线AO匀速运动,设点P的运动时间为t秒.过点P与直线AB垂直的直线与y轴交于点E. 如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm.
如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm.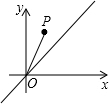 如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.
如图,在平面直角坐标系中,点P的坐标为(1,2),将线段OP沿y轴正方向移动m(m>0)个单位长度至O′P′,以O′P′为直角边在第一象限内作等腰直角△O′P′Q,若点Q在直线y=x上,则m的值为2或3.