题目内容
3.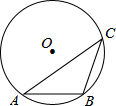 如图,⊙O中,点C是优弧ACB上一点(不与A、B重合),cosC=$\frac{4}{5}$,弦AB=6,则半径r=5.
如图,⊙O中,点C是优弧ACB上一点(不与A、B重合),cosC=$\frac{4}{5}$,弦AB=6,则半径r=5.
分析 首先构造直径所对圆周角,利用圆周角定理得出∠D=∠C,再由cosC=$\frac{4}{5}$可得出AD的长,进而可得出结论.
解答  解:连接AO并延长到圆上一点D,连接BD,
解:连接AO并延长到圆上一点D,连接BD,
∵AD为⊙O直径,
∴∠ABD=90°.
∵∠D=∠C,
∴cosD=cosC=$\frac{4}{5}$.
设BD=4x,则AD=5x,
在Rt△ABD中,
∵AB2+BD2=AD2,即62+(4x)2=(5x)2,解得x=2,
∵AD=10,
∵⊙O的半径为5.
故答案为:5.
点评 此题主要考查了勾股定理以及锐角三角函数的定义和圆周角定理、解直角三角形,根据已知构造直角ABD是解题关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.点P(-1,2)关于x轴对称点的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
18.一块蛋糕,一只猴子第一天吃了一半,第二天吃了剩下的一半,第三天又吃了剩下的一半,这样继续下去,则第五天这只小猴子吃了后,余下这块蛋糕的( )
| A. | $\frac{1}{32}$ | B. | 1-$\frac{1}{32}$ | C. | $\frac{1}{16}$ | D. | 1-$\frac{1}{16}$ |
 如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
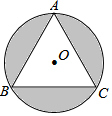 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.