题目内容
2.已知,△ABC是半径为1的⊙O的内接三角形,AB、AC的长分别为1、$\sqrt{2}$,求∠BAC的度数.分析 根据题意画出图形,作出辅助线,由于AC与AB在圆心的同侧还是异侧不能确定,故应分两种情况进行讨论.
解答 解:分别作OD⊥AB,OE⊥AC,垂足分别是D、E如图所示:
∵OE⊥AC,OD⊥AB,
∴AE=$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,AD=$\frac{1}{2}$AB=$\frac{1}{2}$,
在Rt△AOE和Rt△AOD中,
sin∠AOE=$\frac{AE}{AO}$=$\frac{\sqrt{2}}{2}$,sin∠AOD=$\frac{AD}{AO}$=$\frac{1}{2}$,
∴∠AOE=45°,∠AOD=30°,
∴∠BAO=60°,∠CAO=90°-45°=45°,
∴∠BAC=45°+60°=105°,或∠BAC′=60°-45°=15°.
∴∠BAC=15°或105°.
故答案是:15°或105°.
点评 本题考查的是垂径定理及直角三角形的性质,解答此题时进行分类讨论,不要漏解.

练习册系列答案
相关题目
5.能说明命题“若x(x+1)(x-2)=0,则x=0”是假命题的反例是( )
| A. | x=0 | B. | x=-2 | C. | x=1 | D. | x=-1 |
6.点P(-1,2)关于x轴对称点的坐标为( )
| A. | (1,-2) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
17.王先生清明节期间驾车游玩,每次加油都把油箱加满.如表记录了该车相邻两次加油时的相关数据:
注:“累计里程”指汽车从出厂开始累计行驶的路程.
根据数据,王先生计算出这段时间内该车行驶一百公里的平均耗油量大约是( )
| 加油时间 | 油箱加油量(升) | 加油时的累计里程(公里) |
| 2016年3月31日 | 30 | 87006 |
| 2016年4月3日 | 48 | 87606 |
根据数据,王先生计算出这段时间内该车行驶一百公里的平均耗油量大约是( )
| A. | 7升 | B. | 8升 | C. | 9升 | D. | 10升 |
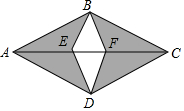 如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块?
如图是某房间木地板的一个图案,其中AB=BC=CD=DA,BE=DE=DF=FB,图案由有花纹的全等三角形木块(阴影部分)和无花纹的全等三角形木块(中间部分)拼成,这个图案的面积是0.05m2.若房间的面积是23m2,问最少需要有花纹的三角形木块和无花纹的木块各多少块? 如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
如图,A、B在直线l异侧,在直线l上取一点P,使PA+PB最小.
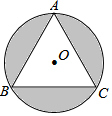 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.