题目内容
20.已知$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$=1-$\frac{1}{100}$
则方程$\frac{x}{1×2}$+$\frac{x}{2×3}$+$\frac{x}{3×4}$+$\frac{x}{4×5}$+…+$\frac{x}{2015×2016}$=2015的解是多少?
分析 根据题中给出的例子把原式进行化简,求出x的值即可.
解答 解:原方程可变为($\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+$\frac{1}{4×5}$+…+$\frac{1}{2015×2016}$)x=2015,
即(1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2015}$-$\frac{1}{2016}$)x=2015,
故(1-$\frac{1}{2016}$)x=2015,解得x=2016.
点评 本题考查的是解一元一次方程与有理数的混合运算,先根据题意把原方程进行化简是解答此题的关键.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
9.方程x2-2x=0的解为( )
| A. | x=2 | B. | x=0 | C. | x1=0 或 x2=2 | D. | x1=0 或 x2=-2 |

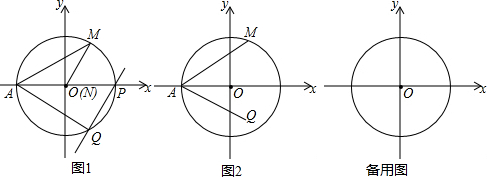
 如图所示:在长方形中放置了6个正方形,图中给出了相关数据,请你仔细观察图形,利用方程思想求出图中的阴影部分的面积的和.
如图所示:在长方形中放置了6个正方形,图中给出了相关数据,请你仔细观察图形,利用方程思想求出图中的阴影部分的面积的和.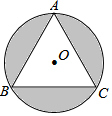 如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$.
如图,正△ABC内接于半径是2的圆,那么阴影部分的面积是4π-3$\sqrt{3}$. 如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm.
如图是一块长、宽、高分别为4cm、2cm和1cm的长方体木块,一只蚂蚁要从长方体木块的-个顶点A处,沿着长方体木块的表面爬到长方体木块上和顶点A相对的顶点B处吃食物,那么它需要爬行的最短路径的长是5cm.