题目内容
13.小明做二次根式化简时,发现一些二次根式的被开方数仍含有根号,比如:$\sqrt{3+2\sqrt{2}}$,善于思考的小明进行了如下探索:要将$\sqrt{a±2\sqrt{b}}$化简,如果能找到两个数m、n,使m2+n2=a且$mn=\sqrt{b}$,则将$a±2\sqrt{b}$将变成m2+n2±2mn,即变成(m±n)2开方,从而使得$\sqrt{a±2\sqrt{b}}$化简.例如:$\sqrt{3+2\sqrt{2}}=\sqrt{{{(\sqrt{2})}^2}+{1^2}+2\sqrt{2}}=\sqrt{{{(\sqrt{2}+1)}^2}}=\sqrt{2}+1$
请仿照上例化简:(1)$\sqrt{7+2\sqrt{10}}$(2)$\sqrt{5-2\sqrt{6}}$.
分析 (1)根据阅读材料和完全平方公式以及二次根式的性质解答;
(2)根据完全平方公式以及二次根式的性质解答.
解答 解:(1)原式=$\sqrt{(\sqrt{5}{)^2}+2\sqrt{5}•\sqrt{2}+(\sqrt{2}{)^2}}$
=$\sqrt{(\sqrt{5}+\sqrt{2}{)^2}}$
=$\sqrt{5}+\sqrt{2}$;
(2)原式=$\sqrt{(\sqrt{3}{)^2}-2\sqrt{3}•\sqrt{2}+(\sqrt{2}{)^2}}$
=$\sqrt{(\sqrt{3}-\sqrt{2}{)^2}}$
=$\sqrt{3}-\sqrt{2}$.
点评 本题考查的是二次根式的化简求值,掌握二次根式的性质和完全平方公式是解题的关键.

练习册系列答案
相关题目
4.已知点A(-3,m)与点B(2,n)是直线y=-$\frac{2}{3}$x+b上的两点,则m与n的大小关系是( )
| A. | m>n | B. | m=n | C. | m<n | D. | 无法确定 |
5.若|1-x|+$\sqrt{x-1}$=0,则x的取值范围是( )
| A. | x≥1 | B. | x=1 | C. | x≤1 | D. | x>1 |
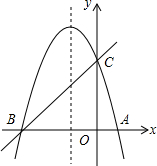 如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.
如图,已知抛物线y=ax2+bx+c(a≠0)经过A,B,C三点,点B的坐标为(-3,0),且OC=3OA,直线y=x+m经过B、C两点.