题目内容

1．若|x-3y+5|+（3x+y-5）2+$\sqrt{x+y-3z}$=0，求$\sqrt{x+y+z}$的值．

分析 直接利用偶次方的性质以及绝对值的性质和二次根式的性质得出方程组进而解方程得出答案．

解答 解：∵|x-3y+5|+（3x+y-5）2+$\sqrt{x+y-3z}$=0，
∴$\left\{\begin{array}{l}{x-3y+5=0}\\{3x+y-5=0}\\{x+y-3z=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=1}\end{array}\right.$，
∴$\sqrt{x+y+z}$=$\sqrt{4}$=2．

点评 此题主要考查了偶次方的性质以及绝对值的性质和二次根式的性质，正确得出关于x，y，z的等式是解题关键．

练习册系列答案
相关题目
11．如图所示，已知在直角坐标系中，点B（3，1），过点B作AB∥x轴，交直线y=x于点A，作BC⊥x轴于点C．动点P从O点出发，沿x轴正方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线OA，垂足为Q．设P点移动的时间为t秒（0＜t＜4），△OPQ与直角梯形OABC重叠部分的面积为S．
（1）求经过O、A、B三点的抛物线解析式；
（2）求S与t的函数关系式；
（3）连接AC、QC，当t为何值时，CQ平分∠ACO？
（4）将△OPQ绕着点P顺时针旋转90°，是否存在t，使得△OPQ的顶点O或Q在抛物线上？若存在，直接写出t的值；若不存在，请说明理由．
12．计算：$\sqrt{40}$-5$\sqrt{\frac{2}{5}}$=$\sqrt{10}$．
9．求不等式组$\left\{\begin{array}{l}{x-1≥1-x}\\{x+8＞4x-1}\end{array}\right.$的解集，并判断x=$\frac{\sqrt{5}}{2}$是否为该不等式组的一个解．
16．下列运算中，正确的是（　　）
A．a2+a3=a5B．$\sqrt{4}$=±2C．a2•a3=a5D．（2a）3=6a3
6．实验中学为了鼓励同学们参加体育锻炼，决定为每个班级配备排球或足球一个，已知一个排球和两个足球需要140元，两个排球和一个足球需要230元．
（1）求排球和足球的单价．
（2）全校共有50个班，学校准备拿出不超过2400元购买这批排球和足球，并且要保证排球的数量不超过足球数量的$\frac{3}{7}$，问：学校共有几种购买方案？哪种购买方案总费用最低？
13．小明做二次根式化简时，发现一些二次根式的被开方数仍含有根号，比如：$\sqrt{3+2\sqrt{2}}$，善于思考的小明进行了如下探索：要将$\sqrt{a±2\sqrt{b}}$化简，如果能找到两个数m、n，使m2+n2=a且$mn=\sqrt{b}$，则将$a±2\sqrt{b}$将变成m2+n2±2mn，即变成（m±n）2开方，从而使得$\sqrt{a±2\sqrt{b}}$化简．
例如：$\sqrt{3+2\sqrt{2}}=\sqrt{{{（\sqrt{2}）}^2}+{1^2}+2\sqrt{2}}=\sqrt{{{（\sqrt{2}+1）}^2}}=\sqrt{2}+1$
请仿照上例化简：（1）$\sqrt{7+2\sqrt{10}}$（2）$\sqrt{5-2\sqrt{6}}$．
10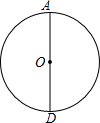．如图，AD为⊙O直径，作⊙O的内接正三角形ABC，作法错误的是（　　）
A．作OD的中垂线，交⊙O于B、C，连结AB，AC
B．以D点为圆心，OD长为半径作圆弧，交圆于点B，C，连结AB，BC，CA
C．以A点为圆心，AO长为半径作圆弧，交圆于点E，F，分别以E，F为圆心作圆弧，交圆于不同于点A的两点B，C，连结AB，BC，CA
D．作AD的中垂线，交⊙O于B、C，连结AB，AC
11．已知一元二次方程x2-5x+3=0，则该方程根的情况是（　　）
A．有两个不相等的实数根B．有两个相等的实数根
C．无实数根D．无法确定

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网