题目内容
3.对于平面直角坐标系中的点P(a,b),若点P′的坐标为(a+$\frac{b}{k}$,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k属派生点”.若点Q(0,4$\sqrt{3}$),点A在直线y=-4$\sqrt{3}$x上,点A是点B的“-$\sqrt{3}$属派生点”,当直线QB与x轴平行时,求点B的坐标.分析 结合已知条件设点B的坐标为(m,4$\sqrt{3}$),点A的坐标为(n,-4$\sqrt{3}$n).根据“k属派生点”的定义即可得出关于m、n的二元一次方程组,解方程组即可得出结论.
解答 解:∵点Q(0,4$\sqrt{3}$),直线QB与x轴平行,点A在直线y=-4$\sqrt{3}$x上,
∴设点B的坐标为(m,4$\sqrt{3}$),点A的坐标为(n,-4$\sqrt{3}$n).
依题意得:$\left\{\begin{array}{l}{n=m+\frac{4\sqrt{3}}{-\sqrt{3}}}\\{-4\sqrt{3}n=-\sqrt{3}m+4\sqrt{3}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{m=4}\\{n=0}\end{array}\right.$.
故点B的坐标为(4,4$\sqrt{3}$).
点评 本题考查了一次函数图象上点的坐标特征以及解二元一次方程组,解题的关键是得出关于m、n的二元一次方程组.本题属于基础题,难度不大,解决该题型题目时,结合“k属派生点”的定义得出方程组是关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
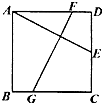 如图,已知正方形ABCD的边长为2,点E为CD的中点,点F、G分别在AD、BC上,FG⊥AE,则FG的长为$\sqrt{5}$.
如图,已知正方形ABCD的边长为2,点E为CD的中点,点F、G分别在AD、BC上,FG⊥AE,则FG的长为$\sqrt{5}$.
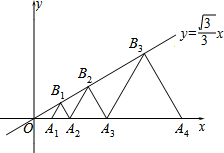 如图,在平面直角坐标系中,点B1,B2,B3,…是直线y=$\frac{\sqrt{3}}{3}$x上的第一象限内的点;点A1,A2,A3,…,在x轴正半轴上,且△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若A1的坐标为(1,0),则点么B5的坐标是(24,8$\sqrt{3}$).
如图,在平面直角坐标系中,点B1,B2,B3,…是直线y=$\frac{\sqrt{3}}{3}$x上的第一象限内的点;点A1,A2,A3,…,在x轴正半轴上,且△A1B1A2,△A2B2A3,△A3B3A4,…均为等边三角形,若A1的坐标为(1,0),则点么B5的坐标是(24,8$\sqrt{3}$).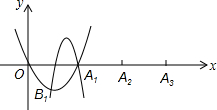 如图,已知在平面直角坐标系中,x轴上依次有点A1(2,0),A2(4,0),A3(6,0),…,抛物线l1:y=x2+bx+c经过原点及A1,顶点为B1;抛物线l2经过B1和A1,且形状与抛物线l1的形状相同,开口方向相反;抛物线l3经过A1和A2,且形状与抛物线l2的形状相同,开口方向相反,顶点为B2:抛物线l4经过B2和A2,且形状与抛物线l3的形状相同,开口方向相反:抛物线l5经过A2和A3,且形状与抛物线l4的形状相同,开口方向相反,顶点为B3:依此类推…
如图,已知在平面直角坐标系中,x轴上依次有点A1(2,0),A2(4,0),A3(6,0),…,抛物线l1:y=x2+bx+c经过原点及A1,顶点为B1;抛物线l2经过B1和A1,且形状与抛物线l1的形状相同,开口方向相反;抛物线l3经过A1和A2,且形状与抛物线l2的形状相同,开口方向相反,顶点为B2:抛物线l4经过B2和A2,且形状与抛物线l3的形状相同,开口方向相反:抛物线l5经过A2和A3,且形状与抛物线l4的形状相同,开口方向相反,顶点为B3:依此类推…