题目内容
8. 如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.
如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.
分析 由等腰三角形的性质知∠ABC=∠ACB=75°,根据旋转的性质得出∠ECD=∠BCA=75°、∠EDC=∠BAC=30°、AC=DC,从而求得∠CDA=∠CAD=$\frac{180°-75°}{2}$=52.5°,根据∠ADE=∠CDA-∠EDC可得答案.
解答 解:∵△ABC是等腰三角形,且∠BAC=30°,
∴∠ABC=∠ACB=75°,
∵△ABC绕点C旋转得到△DEC,
∴∠ECD=∠BCA=75°,∠EDC=∠BAC=30°,AC=DC,
∴∠CDA=∠CAD=$\frac{180°-75°}{2}$=52.5°,
∴∠ADE=∠CDA-∠EDC=22.5°,
故答案为:22.5°.
点评 本题考查了转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
相关题目
18.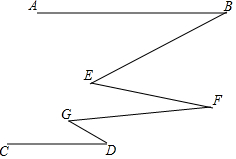 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )| A. | ∠D=∠F=∠B | B. | ∠B+∠F+∠D=60° | C. | ∠B+∠F+∠D=120° | D. | GD∥EF |
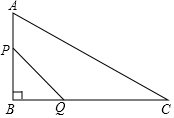 如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB匀速移动到点B,动点Q从点B开始沿边BC匀速移动到点B,如果P、Q两点分别从A、B两点同时出发,同时到达终点,则线段PQ的中点的运动路径长为6$\sqrt{5}$mm.
如图,在△ABC中,∠B=90°,AB=12mm,BC=24mm,动点P从点A开始沿边AB匀速移动到点B,动点Q从点B开始沿边BC匀速移动到点B,如果P、Q两点分别从A、B两点同时出发,同时到达终点,则线段PQ的中点的运动路径长为6$\sqrt{5}$mm.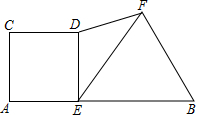 如图,已知线段AB=10,点E在线段AB上运动(不与A、B重合),分别以AE、EB为边在AB的同侧作正方形ACDE和等边△BEF,连接DF,则DF2的最小值为50-25$\sqrt{3}$.
如图,已知线段AB=10,点E在线段AB上运动(不与A、B重合),分别以AE、EB为边在AB的同侧作正方形ACDE和等边△BEF,连接DF,则DF2的最小值为50-25$\sqrt{3}$.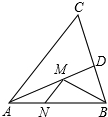 如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.
如图,在锐角△ABC中,AB=6,∠BAC=45°,∠BAC的平分线交BC于点D,M,N分别是AD和AB上的动点,则BM+MN的最小值是3$\sqrt{2}$.