题目内容
13.已知$\frac{1}{4}$x2+y2-x+y+$\frac{5}{4}$=0,求x1006y2013的值.分析 直接利用完全平方公式将原式变形得出x,y的值,进而得出答案.
解答 解:∵$\frac{1}{4}$x2+y2-x+y+$\frac{5}{4}$=0,
∴($\frac{1}{2}$x-1)2+(y+$\frac{1}{2}$)2=0,
∴x=2,y=-$\frac{1}{2}$,
∴x1006y2013=(xy)1006×y1007=[2×(-$\frac{1}{2}$)]1006×(-$\frac{1}{2}$)1007=-$\frac{1}{{2}^{1007}}$.
点评 此题主要考查了配方法的应用,正确应用完全平方公式是解题关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
5.关于x的方程(m-2)x2+2x+1=0有实数根,则偶数m的最大值为( )
| A. | -2 | B. | 0 | C. | 2 | D. | 4 |
3.15:40时,时针与分针所成角的度数是( )
| A. | 120 | B. | 130 | C. | 140 | D. | 150 |
 如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.
如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.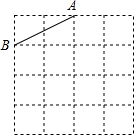 已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题:
已知格点△ABC的一边AB如图,方格中小正方形的边长为1,若另一边AC=$\sqrt{10}$,在如图中画出△ABC(只需画出满足的一个)并回答如下问题: 如图,点A,B,C,D在一次函数y=-2x+m的图象上,它们的横坐标分别为-1,0,3,7,分别过这些点作x轴、y轴的垂线,得到三个矩形,那么这三个矩形的周长和为48.
如图,点A,B,C,D在一次函数y=-2x+m的图象上,它们的横坐标分别为-1,0,3,7,分别过这些点作x轴、y轴的垂线,得到三个矩形,那么这三个矩形的周长和为48.