题目内容
19.已知y=|2x+6|+|x-1|-4|x+1|,求y的最大值6.分析 先分别令2x=6=0,x-1=0,x+1=0求得对应的x的值,然后将x的值分为四段进行分类解答即可.
解答 解:令2x+6=0,x-1=0,x+1=0,
解得:x=-3,x=1,x=-1.
当x≤-3时,原式=-2x-6+1-x-4(-x-1)=-2x-6+1-x+4x+4=x-1,
当x=-3是有最大值,最大值为-4.
当-3<x≤-1时,原式=2x+6+1-x+4x+4=5x+11,
所以当x=-1时,有最大值,最大值为6.
当-1≤x≤1时,原式=2x+6+1-x-4x-4=-3x+3,
所以当x=-1是,原式有最大值,最大值为6.
当x≥1时,原式=2x+6+x-1-4x-4=-x+1,
∴当x=1时,原式有最大值,最大值为0.
综上所述,y的最大值为6.
故答案为:6.
点评 本题主要考查的是绝对值的性质,分类讨论是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.
如图,△ABC中,AB=8,AC=6,BC=10,作BC的垂直平分线DE交AB于点D,则AD=$\frac{7}{4}$.



 如图,△ABC内接于⊙O,∠ABC=60°,D为$\widehat{AC}$的中点.若CD=1,则⊙O的直径为2.
如图,△ABC内接于⊙O,∠ABC=60°,D为$\widehat{AC}$的中点.若CD=1,则⊙O的直径为2. 如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.
如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.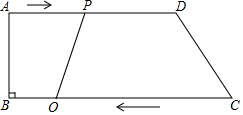 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.