题目内容
18.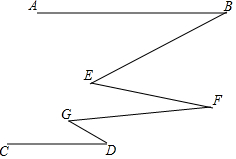 如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )
如图,AB∥CD,∠E=∠G=30°,则下列判断中正确的是( )| A. | ∠D=∠F=∠B | B. | ∠B+∠F+∠D=60° | C. | ∠B+∠F+∠D=120° | D. | GD∥EF |
分析 过E作EM∥AB,过F作FN∥AB,过G作GQ∥AB,推出AB∥EM∥FN∥GQ∥CD,根据平行线的性质得出∠B=∠BEM,∠EFN=∠MEF,∠NFG=∠QGF,∠D=∠DGQ,求出∠B+∠EFG+∠D=∠BEF+∠FGD,即可得出选项.
解答 解:
过E作EM∥AB,过F作FN∥AB,过G作GQ∥AB,
∵AB∥CD,
∴AB∥EM∥FN∥GQ∥CD,
∴∠B=∠BEM,∠EFN=∠MEF,∠NFG=∠QGF,∠D=∠DGQ,
∴∠B+∠EFN+∠NFG+∠D=∠BEM+∠FEM+∠QGF+∠DGQ,
∴∠B+∠EFG+∠D=∠BEF+∠FGD,
∵∠BEF=∠FGD=30°
∴∠B+∠EFG+∠D=60°,
故选B.
点评 本题考查了平行线的性质和判定,能正确作出辅助线和求出∠B+∠EFG+∠D=∠BEF+∠FGD是解此题的关键.

练习册系列答案
相关题目
6.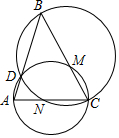 如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
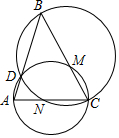 如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )
如图,在锐角△ABC中,∠ACB=60°,点D为线段AB上的一点,△ACD的外接圆交BC于点M,△BCD的外接圆交AC于点N,则$\frac{CM}{CA}$+$\frac{CN}{CB}$=( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
3.15:40时,时针与分针所成角的度数是( )
| A. | 120 | B. | 130 | C. | 140 | D. | 150 |
 如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.
如图,将等腰三角形ABC绕点C旋转,使底边BC落在腰AC上,若∠BAC=30°,则∠ADE=22.5°.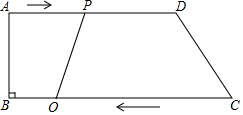 如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.
如图所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm.动点P从点A出发沿AD方向向点D以1cm/s的速度运动.动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动.点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动.设运动时间为t.