题目内容
16.如图,已知抛物线$y=\frac{a}{3}(x+1)(x-3)(a$为常数,且a>0)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C(0,$-\sqrt{3}$).点P是线段BC上一个动点,点P横坐标为m.(1)a的值为$\sqrt{3}$;
(2)判断△ABC的形状,并求出它的面积;
(3)如图1,过点P作y的平行线,交抛物线于点D.
①请你探究:是否存在实数m,使四边形OCDP是平行四边形?若存在,求出m的值;若不存在,请说明理由;
②过点D作DE⊥BC于点E,设△PDE的面积为S,求S的最大值.
(4)如图2,F为AB中点,连接FP.一动点Q从F出发,沿线段FP以每秒1个单位的速度运动到P,再沿着线段PC以每秒2个单位的速度运动到C后停止.若点Q在整个运动过程中的时间为t秒,请直接写出t的最小值及此时点P的坐标.

分析 (1)直接把C点坐标代入$y=\frac{a}{3}(x+1)(x-3)(a$可求出a的值;
(2)利用抛物线与x轴的交点问题得到A(-1,0),B(3,0),则根据正切的定义和特殊角的三角函数值可求出∠ACO=30°,∠BCO=60°,则∠ACB=90°,于是可判断△ACB为直角三角形,然后根据三角形面积公式计算S△ACB;
(3)①先利用待定系数法求出直线BC的解析式为y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$,则可设点P的坐标为(m,m-$\sqrt{3}$),D(m,$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$),易得PD=-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$m,根据平行四边形的判定,当PD=OC时,四边形OCDP是平行四边形,则-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$m=$\sqrt{3}$,由于此方程没有实数解,于是可判断不存在实数m,使四边形OCDP是平行四边形;
②如图1,先利用PD∥OC得到∠EPD=∠OCB=60°,根据特殊角的三角函数值得到PE=$\frac{1}{2}$PD,DE=$\sqrt{3}$PE=$\frac{\sqrt{3}}{2}$PD,则S=$\frac{\sqrt{3}}{8}$PD2,再利用二次函数的性质得到PD的最大值为$\frac{3\sqrt{3}}{4}$,于是可得到S的最大值;
(4)过P点作过C且平行于x轴的直线于点H,如图2,作FH′⊥CH于H′,交BC于P′,利用∠PCH=30°得到PH=$\frac{1}{2}$PC,根据速度公式得到t=$\frac{PF}{1}$+$\frac{PC}{2}$,则t=PF+PH,利用两点之间线段最短可判断当F、P、H共线时,PF+PH最小,此时t=PH′=$\sqrt{3}$,然后求出F(1,0)后确定P′点的坐标即可.
解答 解:(1)把C(0,$-\sqrt{3}$)代入$y=\frac{a}{3}(x+1)(x-3)(a$得$\frac{a}{3}$•1•(-3)=-$\sqrt{3}$,解得a=$\sqrt{3}$,
故答案为$\sqrt{3}$;
(2)抛物线解析式为y=$\frac{\sqrt{3}}{3}$(x+1)(x-3),即y=$\frac{\sqrt{3}}{3}$x2-$\frac{2\sqrt{3}}{3}$x-$\sqrt{3}$,
当y=0时,$\frac{\sqrt{3}}{3}$(x+1)(x-3)=0,解得x1=-1,x2=3,则A(-1,0),B(3,0),
而C(0,-$\sqrt{3}$),
在Rt△AOC中,∵tan∠AOC=$\frac{OA}{OC}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠ACO=30°,
在Rt△OBC中,∵tan∠BCO=$\frac{OB}{OC}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴∠BCO=60°,
∴∠ACB=30°+60°=90°,
∴△ACB为直角三角形,
S△ACB=$\frac{1}{2}$•(3+1)•$\sqrt{3}$=2$\sqrt{3}$;
(3)①不存在.理由如下:
设BC的解析式为y=kx+b,
把B(3,0),C(0,-$\sqrt{3}$)代入得$\left\{\begin{array}{l}{3k+b=0}\\{c=-\sqrt{3}}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{\sqrt{3}}{3}}\\{b=-\sqrt{3}}\end{array}\right.$,
∴直线BC的解析式为y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$,
设点P的坐标为(m,m-$\sqrt{3}$),则D(m,$\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$),
∴PD=$\frac{\sqrt{3}}{3}$m-$\sqrt{3}$-($\frac{\sqrt{3}}{3}$m2-$\frac{2\sqrt{3}}{3}$m-$\sqrt{3}$)=-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$m,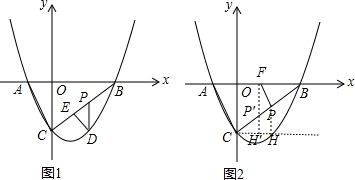
∵PD∥OC,
∴当PD=OC时,四边形OCDP是平行四边形,
即-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$m=$\sqrt{3}$,
整理得m2-3m+3=0,△=(-3)2-4×3<0,方程没有实数解,
∴不存在实数m,使四边形OCDP是平行四边形;
②如图1,∵PD∥OC,
∴∠EPD=∠OCB=60°,
∴∠PDE=30°,
∴PE=$\frac{1}{2}$PD,DE=$\sqrt{3}$PE=$\frac{\sqrt{3}}{2}$PD,
∴S=$\frac{1}{2}$PE•DE=$\frac{\sqrt{3}}{8}$PD2,
∵PD=-$\frac{\sqrt{3}}{3}$m2+$\sqrt{3}$m=-$\frac{\sqrt{3}}{3}$(m-$\frac{3}{2}$)2+$\frac{3\sqrt{3}}{4}$,
∴PD的最大值为$\frac{3\sqrt{3}}{4}$,
∴S的最大值为$\frac{\sqrt{3}}{8}$×($\frac{3\sqrt{3}}{4}$)2=$\frac{27\sqrt{3}}{128}$;
(4)过P点作过C且平行于x轴的直线于点H,如图2,作FH′⊥CH于H′,交BC于P′,
∵∠OCB=60°,
∴∠PCH=30°,
∴PH=$\frac{1}{2}$PC,
∵t=$\frac{PF}{1}$+$\frac{PC}{2}$,
∴t=PF+PH,
∴当F、P、H共线时,PF+PH最小,此时t=FH′=$\sqrt{3}$,
∵F为AB中点,
∴F(1,0),
当x=1时,y=$\frac{\sqrt{3}}{3}$x-$\sqrt{3}$=-$\frac{2\sqrt{3}}{3}$,
∴t的最小值为$\sqrt{3}$,此时点P的坐标为(1,-$\frac{2\sqrt{3}}{3}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数的图象上点的坐标特征、二次函数的性质和平行四边形的判定;会利用待定系数求函数解析式;会解直角三角形,记住特殊角的三角函数值;理解坐标与图形性质.

 备战中考寒假系列答案
备战中考寒假系列答案| 选手 | 甲 | 乙 | 丙 |
| 平均数 | 9.3 | 9.3 | 9.3 |
| 方差 | 0.026 | a | 0.032 |
| A. | 0 | B. | 0.020 | C. | 0.030 | D. | 0.035 |
 如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )
如图,已知:CD∥BE,∠1=68°,那么∠B的度数为( )| A. | 68° | B. | 102° | C. | 110° | D. | 112° |
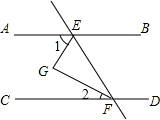 如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )
如图,直线AB∥CD,EG,FG分别平分∠AEF和∠EFC,如果∠1=70°,那么∠2等于( )| A. | 40° | B. | 35° | C. | 25° | D. | 20° |
| A. | 60.8×108 | B. | 6.08×109 | C. | 6.8×109 | D. | 608.8×107 |
 如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )
如图,若AB是⊙O的直径,CD是⊙O的弦,∠ABD=58°,则∠BCD的度数为( )| A. | 32° | B. | 58° | C. | 64° | D. | 116° |