题目内容
6.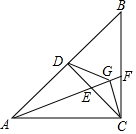 如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.
如图,在等腰直角三角形ABC中,AC=BC,AB=4$\sqrt{5}$,D是AB的中点,连结DC,E为DC中点,连接AE,延长AE交BC于F,过点C作CG⊥AF,垂足是G,连接DG,则∠DGA=45°,DG=2$\sqrt{2}$.
分析 根据等腰直角三角形的性质得到CD⊥AB,CD=$\frac{1}{2}$AB=2$\sqrt{5}$,∠ACD=∠BCD=45°,推出点A,C,G,D四点共圆,根据圆周角定理得到∠DGA=∠ACD=45°,过D作DH⊥AF于H,得到△DHG是等腰直角三角形,求得DE=$\frac{1}{2}$CD=$\sqrt{5}$,根据勾股定理得到AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5,根据三角形的面积公式得到DH=$\frac{AD•DE}{AE}$=2,于是得到结论.
解答 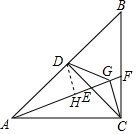 解:∵在等腰直角三角形ABC中,AC=BC,D是AB的中点,
解:∵在等腰直角三角形ABC中,AC=BC,D是AB的中点,
∴CD⊥AB,CD=$\frac{1}{2}$AB=2$\sqrt{5}$,∠ACD=∠BCD=45°,
∵CG⊥AF,
∴∠ADC=∠AGC=90°,
∴点A,C,G,D四点共圆,
∴∠DGA=∠ACD=45°,
过D作DH⊥AF于H,
∴△DHG是等腰直角三角形,
∵E为DC中点,
∴DE=$\frac{1}{2}$CD=$\sqrt{5}$,
∴AE=$\sqrt{A{D}^{2}+D{E}^{2}}$=5,
∴DH=$\frac{AD•DE}{AE}$=2,
∴DG=$\sqrt{2}$DH=2$\sqrt{2}$.
故答案为:45°,2$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质和判定,四点共圆,正确的作出辅助线是解题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
14.根据如图所示,对a、b、c三种物体的重量判断正确的是( )


| A. | a<b | B. | b<c | C. | a>c | D. | a<c |
11.把方程$\frac{1}{3}$x2-x-4=0左边配成一个完全平方式,得到的方程是( )
| A. | (x-$\frac{3}{2}$)2=$\frac{38}{4}$ | B. | (x-$\frac{3}{2}$)2=$\frac{38}{4}$ | C. | (x+$\frac{3}{2}$)2=$\frac{57}{4}$ | D. | (x-$\frac{3}{2}$)2=$\frac{57}{4}$ |
15.对于$\sqrt{5}$-2,下列说法中正确的是( )
| A. | 它是一个无理数 | B. | 它比0小 | ||
| C. | 它不能用数轴上的点表示出来 | D. | 它的相反数为$\sqrt{5}$+2 |
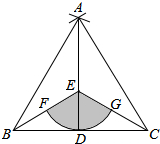 如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.
如图,点D是线段BC的中点,分别以点B,C为圆心,BC长为半径画弧,两弧相交于点A,连接AB,AC,AD,点E为AD上一点,连接BE,CE.  如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.
如图,在等腰三角形ABC中,AB=2,∠A=90°,点E为腰AB的中点,点F在底边BC上,且FE⊥CE,则△BEF的面积$\frac{1}{6}$.