题目内容
18.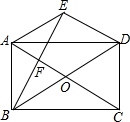 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
分析 (1)先证明四边形AODE是平行四边形,再由矩形的性质得出OA=OC=OD,即可得出四边形AODE是菱形;
(2)连接OE,由菱形的性质得出AE=OB=OA,证明四边形AEOB是菱形,得出AB=OB=OA,证出△AOB是等边三角形,得出∠AOB=60°,再由平角的定义即可得出结果.
解答 (1)证明:∵AE∥BD,ED∥AC,
∴四边形AODE是平行四边形,
∵四边形ABCD是矩形,
∴OA=OC=$\frac{1}{2}$AC,OB=OD=$\frac{1}{2}$BD,AC=BD,
∴OA=OC=OD,
∴四边形AODE是菱形;
(2)解: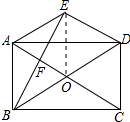 连接OE,如图所示:
连接OE,如图所示:
由(1)得:四边形AODE是菱形,
∴AE=OB=OA,
∵AE∥BD,
∴四边形AEOB是平行四边形,
∵BE⊥ED,ED∥AC,
∴BE⊥AC,
∴四边形AEOB是菱形,
∴AE=AB=OB,
∴AB=OB=OA,
∴△AOB是等边三角形,
∴∠AOB=60°,
∴∠AOD=180°-60°=120°.
点评 本题考查了菱形的判定与性质、矩形的性质、等边三角形的判定与性质、平行四边形的判定;熟练掌握矩形的性质和菱形的判定与性质,证明四边形AEOB是菱形再进一步证出△AOB是等边三角形是解决问题(2)的关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
6. 在如图的地板行走,随意停下来时,站在黑色地板上的概率是( )
在如图的地板行走,随意停下来时,站在黑色地板上的概率是( )
 在如图的地板行走,随意停下来时,站在黑色地板上的概率是( )
在如图的地板行走,随意停下来时,站在黑色地板上的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
13.下列命题中,正确的是( )
| A. | 对角线垂直的四边形是菱形 | B. | 矩形的对角线垂直且相等 | ||
| C. | 对角线相等的矩形是正方形 | D. | 位似图形一定是相似图形 |
3.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (-2a2b)3=-8a5b3 | C. | a6÷a3=a2 | D. | a3•a2=a5 |
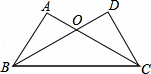 在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.
在△ABC和△DCB中,AC,BD交于点O,AB=DC,AC=BD.求证:(1)△ABC≌△DCB:(2)OB=OC.
 某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像.
某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像. 如图,在Rt△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于点E.若DE=2,BC=3,AC=6,求AE的长.
如图,在Rt△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于点E.若DE=2,BC=3,AC=6,求AE的长.