题目内容
10. 某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像.
某市有一块长为(3a+b)米,宽为(2a+b)米的长方形地块,规划部分计划将阴影部分进行绿化,中间修建一座雕像.(1)请用含a,b的代数式表示绿化面积s;
(2)当a=3,b=2时,求绿化面积s.
分析 (1)由长方形的面积减去正方形的面积表示出S即可;
(2)把a与b的值代入计算即可求出值.
解答 解:(1)根据题意得:S=(3a+b)(2a+b)-(a+b)2=6a2+5ab+b2-a2-2ab-b2=5a2+3ab;
(2)当a=3,b=2时,原式=45+18=63.
点评 此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
5.分解因式8a2-8ab+2b2结果正确的是( )
| A. | 2(2a-b)2 | B. | 8(a-b)2 | C. | 4(a-b)2 | D. | 2(2a+b)2 |
15.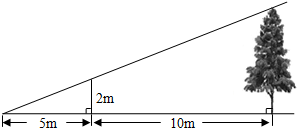 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )| A. | 5m | B. | 6m | C. | 7m | D. | 8m |
19.两条直线相交可以形成2对对顶角,那么同一平面内4条直线最多可以形成对顶角( )
| A. | 8对 | B. | 10对 | C. | 12对 | D. | 16对 |
20.泗阳华润苏果超市准备购进A、B两种品牌的书包共100个,已知两种书包的进价如下表所示,设购进A种书包x个,且所购进的两种书包能全部卖出,获得的总利润为y元.
(1)将表格的信息填写完整;
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
| 品牌 | 购买个数(个) | 进价(元/个) | 售价(元/个) | 获利(元) |
| A | x | 50 | 60 | 10x |
| B | 100-x | 40 | 55 | 15(100-x) |
(2)求y关于x的函数表达式;
(3)如果购进两种书包的总费用不超过4500元且购进B种书包的数量不大于A种书包的3倍,那么超市如何进货才能获利最大?并求出最大利润.
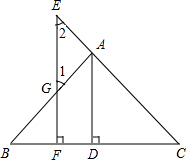 已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
已知:如图AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2,求证:AD平分∠BAC.
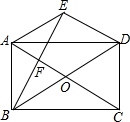 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.