题目内容
7. 如图,在Rt△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于点E.若DE=2,BC=3,AC=6,求AE的长.
如图,在Rt△ABC中,∠C=90°,D是AC边上一点,DE⊥AB于点E.若DE=2,BC=3,AC=6,求AE的长.
分析 根据相似三角形的判定得出两三角形相似,得出比例式,代入求出即可.
解答 解:∵∠C=90°,DE⊥AB,
∴∠AED=∠C=90°,
又∵∠A=∠A,
∴△AED∽△ACB,
∴$\frac{EA}{CA}=\frac{ED}{CB}$,
又∵DE=2,BC=3,AC=6,
∴$\frac{EA}{6}=\frac{2}{3}$,
∴AE=4.
点评 本题考查了相似三角形的性质和判定的应用,能推出△AED∽△ACB是解此题的关键.

练习册系列答案
相关题目
15.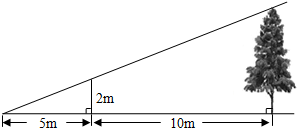 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
 如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )
如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端的影子与树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距5m,与树相距10m,则树的高度为( )| A. | 5m | B. | 6m | C. | 7m | D. | 8m |
12.下列描述不正确的是( )
| A. | 单项式-$\frac{ab}{3}$的系数是-$\frac{1}{3}$,次数是2 | |
| B. | 用一个平面去截一个圆柱,截图的形状可能是一个长方形 | |
| C. | 过七边形的一个顶点有5条对角线 | |
| D. | 五棱柱有7个面,15条棱 |
19.两条直线相交可以形成2对对顶角,那么同一平面内4条直线最多可以形成对顶角( )
| A. | 8对 | B. | 10对 | C. | 12对 | D. | 16对 |
 如图所示,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=35°28′,则∠EGF=72°16′.
如图所示,已知AB∥CD,直线l分别交AB、CD于点E、F,EG平分∠BEF,若∠EFG=35°28′,则∠EGF=72°16′.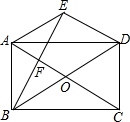 如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.
如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.