题目内容
16. 如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
分析 作CD⊥x轴,构造△AOB≌△CDA,得到DC=OA=2,AD=BO=1,求出C的坐标,把C点坐标代入y=$\frac{k}{x}$(x>0)即可求出k的值.
解答 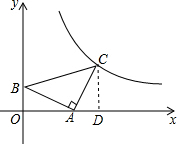 解:∵点A的坐标为(2,0),顶点B的坐标为(0,1),
解:∵点A的坐标为(2,0),顶点B的坐标为(0,1),
∴OA=2,OB=1,
作CD⊥x轴与D,
∴∠BAO+∠CAD=90°,
∵∠BAO+∠ABO=90°,
∴∠CAD=∠ABO,
在△AOB和△CDA中,
$\left\{\begin{array}{l}{∠ABO=∠CAD}\\{∠AOB=∠ADC=90°}\\{AB=AC}\end{array}\right.$,
∴△AOB≌△CDA,
∴DC=OA=2,AD=BO=1,
∴DO=OA+AD=1+2=3;
∴C点坐标为(3,2),
把(3,2)代入y=$\frac{k}{x}$(x>0)得,k=6.
故选D.
点评 本题考查了反比例函数综合题,涉及全等三角形的判定、等腰直角三角形的性质、函数图象上点的坐标特征,有一定难度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.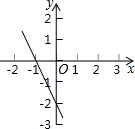 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
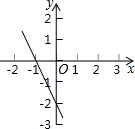 如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )
如图,是函数y=kx+b的图象,当y<-1时,x的取值范围是( )| A. | x<-$\frac{1}{2}$ | B. | x>-$\frac{1}{2}$ | C. | x<-$\frac{1}{4}$ | D. | x>-$\frac{1}{4}$ |
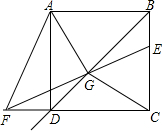 如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG.
如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG. 如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则阴影部分的面积为$\frac{169π}{6}$-$\frac{169\sqrt{3}}{4}$..
如图,在Rt△ABC中,∠ACB=90°,AC=5cm,BC=12cm,将△ABC绕点B顺时针旋转60°,得到△BDE,连接DC交AB于点F,则阴影部分的面积为$\frac{169π}{6}$-$\frac{169\sqrt{3}}{4}$.. 在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.
在直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.且规定,正方形的内部不包含边界上的点.观察如图所示的中心在原点、一边平行于x轴的正方形:边长为1的正方形内部有1个整点,边长为2的正方形内部有1个整点,边长为3的正方形内部有9个整点,…,则边长为8的正方形内部的整点的个数为49.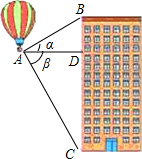 热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)?
热气球的探测器显示,从热气球看一栋楼顶部的仰角α为27°,看这栋楼底部的俯角β为58°,热气球与这栋楼的水平距离为120米,这栋楼有多高(结果取整数)? 如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).