Question

5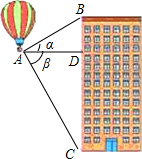．热气球的探测器显示，从热气球看一栋楼顶部的仰角α为27°，看这栋楼底部的俯角β为58°，热气球与这栋楼的水平距离为120米，这栋楼有多高（结果取整数）？
（参考数据：sin27°=0.45，cos27°=0.89，tan27°=0.51，sin58°=0.85，cos58°=0.53，tan58°=1.60）

Answer 1

分析 根据正切的定义分别求出BD、DC的长，求和即可．

解答 解：在Rt△ABD中，tanα=$\frac{BD}{AD}$，
则BD=AD•tanα=120×0.51=61.2，
在Rt△ACD中，tanβ=$\frac{CD}{AD}$，
则CD=AD•tanβ=120×1.60=192，
∴BC=BD+CD=61.2+192=253.2≈253，
答：这栋楼高约为253米．

点评 本题考查的是解直角三角形的应用-仰角俯角问题，正切理解仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．