题目内容
10.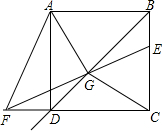 如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG.
如图,正方形ABCD的边长为4,点E、F分别是射线BC和CD延长线上的动点,且BE=DF,连接EF与射线BD交于点G,连接AG、CG.(1)求证:EG=FG;
(2)当△GCE为等边三角形时,求四边形AFDG的面积.
分析 (1)作EH⊥BC交BD于H,由正方形的性质得出AB∥CF,∠BCD=90°,∠EBH=45°,AB⊥BC,证出△BEH是等腰直角三角形,得出BE=EH,证出EH=DF,由平行线的性质得出∠HEG=∠DFG,由AAS证明△GHE≌△GFD,得出对应边相等即可;
(2)过G作CD的平行线,交AD于M,BC于N,由等边三角形的性质得出CN=EN,设CN=EN=x,则CG=CE=2x,GN=$\sqrt{3}$x,作GO⊥CD于O,则GM=GO=CN=x,MN=CD=4得出方程,解方程求出x=2$\sqrt{3}$-2,得出DF=BE=BC-CE=8-4$\sqrt{3}$,四边形AFDG的面积=△ADF的面积+△ADG的面积,即可得出结果.
解答 (1)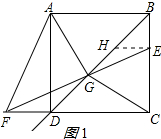 证明:作EH⊥BC交BD于H,如图1所示:
证明:作EH⊥BC交BD于H,如图1所示:
∵四边形ABCD是正方形,
∴AB∥CF,∠BCD=90°,∠EBH=45°,AB⊥BC,
∴△BEH是等腰直角三角形,
∴BE=EH,
∵BE=DF,
∴EH=DF,
∵EH⊥BC,AB∥CF,
∴EH∥CF,
∴∠HEG=∠DFG,
在△GEH和△GFD中,
$\left\{\begin{array}{l}{∠HEG=∠DFG}&{\;}\\{∠EGH=∠FGD}&{\;}\\{EH=DF}&{\;}\end{array}\right.$,
∴△GHE≌△GFD(AAS),
∴EG=FG;
(2)解:过G作CD的平行线,交AD于M,BC于N,如图2所示: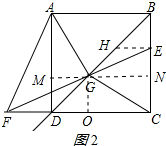
∵△GCE为等边三角形,
∴CN=EN,
设CN=EN=x,则CG=CE=2x,GN=$\sqrt{3}$x,
作GO⊥CD于O,则GM=GO=CN=x,
∵MN=CD=4,
∴x+$\sqrt{3}$x=3,
解得:x=2$\sqrt{3}$-2,
∵DF=BE=BC-CE=4-2x=4-2(2$\sqrt{3}$-2)=8-4$\sqrt{3}$,
∴四边形AFDG的面积=△ADF的面积+△ADG的面积=$\frac{1}{2}$AD(DF+GM)=$\frac{1}{2}$×4(8-4$\sqrt{3}$+2$\sqrt{3}$-2)=12-4$\sqrt{3}$.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、等边三角形的性质等知识;熟练掌握正方形和等边三角形的性质,证明三角形全等是解决问题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2016 | B. | -2016 | C. | $\frac{1}{2016}$ | D. | -$\frac{1}{2016}$ |
| A. | 3a+2b=5ab | B. | a•a4=a4 | C. | (-a3b)2=a6b2 | D. | a6÷a2=a3 |
| 岗位 | 董事长 | 副董事长 | 董事 | 总经理 | 经理 | 部门A | 部门B | 部门C | 部门D | 部门E |
| 人数 | 1 | 1 | 3 | 1 | 4 | 5 | 12 | 20 | 2 | 1 |
| 月工资数(元) | 15000 | 12000 | 10000 | 9000 | 4000 | 2000 | 1800 | 1500 | 800 | 700 |
(2)求月工资的众数;工会主席用众数作为代表数,这是为什么?
(3)求月工资的中位数;税务工作人员用中位数作为代表数,这是为什么?
 如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点且点A在第一象限,是两个函数的一个交点;
如图,反比例函数y=$\frac{k}{2x}$和一次函数y=2x-1,其中一次函数的图象经过(a,b),(a+k,b+k+2)两点且点A在第一象限,是两个函数的一个交点; 如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )