题目内容
6. 如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).
如图,二次函数y=ax2-4ax+2的图象与y轴交于点A,且过点B(3,6).(1)试求二次函数的解析式及点A的坐标;
(2)若点B关于二次函数对称轴的对称点为点C,试求∠CAB的正切值;
(3)若在x轴上有一点P,使得点B关于直线AP的对称点B1在y轴上,试求点P的坐标.
分析 (1)把B(3,6)代入y=ax2-4ax+2,求出a的值,得到二次函数的解析式,进而求出点A的坐标;
(2)先求出抛物线的对称轴,根据对称性得出C点坐标,求出BC=2,AB=5,tan∠CBA=$\frac{4}{3}$,过点C作CH⊥AB于点H,再求出CH=$\frac{8}{5}$,AH=$\frac{19}{5}$,根据正切函数定义即可求出∠CAB的正切值;
(3)由AB=AB1=5,从而点B1的坐标为(0,-3)或(0,7),设P(x,0)根据PB=PB1,分B1的坐标为(0,-3)或(0,7)两种情况利用勾股定理求得x值.
解答 解:(1)∵二次函数y=ax2-4ax+2的图象过点B(3,6),
∴6=9a-12a+2,
解得a=-$\frac{4}{3}$,
所以二次函数的解析式为y=-$\frac{4}{3}$x2+$\frac{16}{3}$x+2,
∵二次函数y=-$\frac{4}{3}$x2+$\frac{16}{3}$x+2的图象与y轴交于点A,
∴点A的坐标为(0,2);
(2)∵y=-$\frac{4}{3}$x2+$\frac{16}{3}$x+2=-$\frac{4}{3}$(x-2)2+$\frac{22}{3}$,
∴对称轴为直线x=2,
∵点B(3,6)关于二次函数对称轴的对称点为点C,
∴C(1,6),
∴BC=2,AB=$\sqrt{{3}^{2}+(6-2)^{2}}$=5,tan∠CBA=$\frac{4}{3}$,
过点C作CH⊥AB于点H,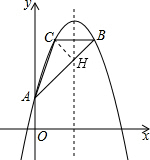
则CH=$\frac{8}{5}$,BH=$\frac{6}{5}$,AH=$\frac{19}{5}$,
∴tan∠CAB=$\frac{CH}{AH}$=$\frac{8}{19}$;
(3)由题意,AB=AB1=5,从而点B1的坐标为(0,-3)或(0,7).
设P(x,0).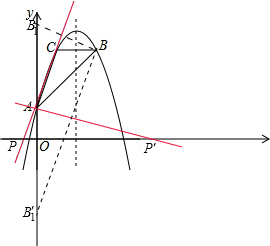
①如果点B1(0,7),
∵点B关于直线AP的对称点B1在y轴上,
∴PB=PB1,即(x-3)2+62=x2+72,
解得x=-$\frac{2}{3}$,即P(-$\frac{2}{3}$,0);
②如果点B1′(0,-3),
∵点B关于直线AP的对称点B1在y轴上,
∴PB=PB1,即(x-3)2+62=x2+32,
解得x=6,即P(6,0);
综上所述,所求点P的坐标为(-$\frac{2}{3}$,0)或(6,0).
点评 本题主要考查待定系数求二次函数解析式、解直角三角形、勾股定理等,求二次函数解析式是基础,构建直角三角形求三角函数值是基本做法,通过勾股定理得出点坐标间联系是关键.

 阅读快车系列答案
阅读快车系列答案 如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )
如图,在平面直角坐标系中,等腰直角三角形ABC的直角顶点A的坐标为(2,0),顶点B的坐标为(0,1),顶点C在第一象限,若函数y=$\frac{k}{x}$(x>0)的图象经过点C,则k的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( )| A. | BE⊥CE | B. | BF∥CE | C. | BE=CF | D. | AB=AC |
| A. | x1<x2 | B. | x2<x1 | ||
| C. | y随x的增大而增大 | D. | 两点有可能在同一象限 |
| A. | -1 | B. | -$\sqrt{2}$ | C. | 0 | D. | 1 |
 如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )
如图是由5个相同的正方体组成的一个立体图形,它的左视图是( )


