题目内容
17.若代数式x3+ax2+bx+8其中有两个因式分别为x+1和x+2,则a+b的值为( )| A. | 8 | B. | 7 | C. | 15 | D. | 21 |
分析 由x3+ax2+bx+8其中有两个因式分别为x+1和x+2得到x=-1、x=-2肯定是关于x的方程x3+ax2+bx+8=0的两个根,所以将其分别代入该方程列出关于a、b的方程组,通过解方程组来求a、b的值,再代入计算即可求解.
解答 解:∵代数式x3+ax2+bx+8其中有两个因式分别为x+1和x+2,
∴x=-1、x=-2肯定是关于x的方程x3+ax2+bx+8=0的两个根,则
$\left\{\begin{array}{l}{-1+a-b+8=0}\\{-8+4a-2b+8=0}\end{array}\right.$,即$\left\{\begin{array}{l}{a-b=-7}\\{4a-2b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=7}\\{b=14}\end{array}\right.$,
a+b=7+14=21.
故选:D.
点评 本题考查了因式分解的意义,根据因式分解的意义得到x=-1、x=-2肯定是关于x的方程x3+ax2+bx+8=0的两个根是解题的难点.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | x3•x-4=x-12 | B. | (x3)3=x6 | C. | 2x2+x=x | D. | (3x)-2=$\frac{1}{9{x}^{2}}$ |
6.某小组7位同学的中考体育测试成绩(满分50分)依次为47,50,49,47,50,48,50,则这组数据的众数与中位数分别是( )
| A. | 50,47 | B. | 50,49 | C. | 49,50 | D. | 50,48 |
 如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,若∠B=60°,则∠EAF=60°.
如图,?ABCD中,AE⊥BC于E,AF⊥DC于F,若∠B=60°,则∠EAF=60°.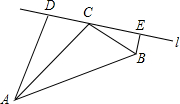 如图,在△ABC中,AC=nBC,且∠ACB=∠ADC=∠BEC=100°,猜想线段DE,AD,BE之间有什么数量关系?并证明你的猜想.
如图,在△ABC中,AC=nBC,且∠ACB=∠ADC=∠BEC=100°,猜想线段DE,AD,BE之间有什么数量关系?并证明你的猜想.