题目内容
7.若$\frac{1}{(2n-1)(2n+1)}=\frac{a}{2n-1}+\frac{b}{2n+1}$,对任意自然数n都成立,则a-b=1.分析 已知等式右边通分并利用同分母分式的加法法则计算,根据题意确定出a与b的值,再代入计算即可求解.
解答 解:∵$\frac{1}{(2n+1)(2n-1)}$=$\frac{a}{2n-1}$+$\frac{b}{2n+1}$=$\frac{a(2n+1)+b(2n-1)}{(2n-1)(2n+1)}$,
∴2n(a+b)+a-b=1,即$\left\{\begin{array}{l}{a+b=0}\\{a-b=1}\end{array}\right.$,
解得:a=$\frac{1}{2}$,b=-$\frac{1}{2}$,
a-b=1.
故答案为:1.
点评 此题考查了分式的加减法,解本题的关键是得到关于a,b的方程组$\left\{\begin{array}{l}{a+b=0}\\{a-b=1}\end{array}\right.$.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
17.若代数式x3+ax2+bx+8其中有两个因式分别为x+1和x+2,则a+b的值为( )
| A. | 8 | B. | 7 | C. | 15 | D. | 21 |
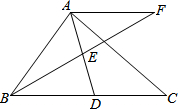 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB. 如图,直线a∥b,∠1=53°,那么∠2、∠3各是多少度?
如图,直线a∥b,∠1=53°,那么∠2、∠3各是多少度?