题目内容
2.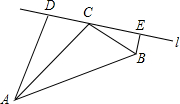 如图,在△ABC中,AC=nBC,且∠ACB=∠ADC=∠BEC=100°,猜想线段DE,AD,BE之间有什么数量关系?并证明你的猜想.
如图,在△ABC中,AC=nBC,且∠ACB=∠ADC=∠BEC=100°,猜想线段DE,AD,BE之间有什么数量关系?并证明你的猜想.
分析 由三角形内角和定理和平角的定义证出∠DAC=∠ECB,证明△ADC∽△CEB,得出对应边成比例$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,得出CE=$\frac{1}{n}$AD,CD=nBE,即可得出结论.
解答 解:猜想:DE=$\frac{1}{n}$AD+nBE.理由如下:
∵∠ADC=100°,
∴∠DAC+∠DCA=80°.
∵∠ACB=100°,
∴∠DCA+∠ECB=80°,
∴∠DAC=∠ECB.
∵∠ADC=∠CEB,
∴△ADC∽△CEB,
∴$\frac{AD}{CE}$=$\frac{CD}{BE}$=$\frac{AC}{BC}$=n,
∴CE=$\frac{1}{n}$AD,CD=nBE,
∴DE=DC+CE=$\frac{1}{n}$AD+nBE;
点评 本题是一道探究题,考查了相似三角形的判定与性质、三角形的内角和定理、平角的定义等知识,考查了探究能力;证明三角形相似得出对应边成比例是解决问题的关键.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
13.下列四幅图案在设计中用到平移变换方式的是( )
| A. |  | B. |  | C. |  | D. |  |
10.计算(-2)0+1的结果( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
17.若代数式x3+ax2+bx+8其中有两个因式分别为x+1和x+2,则a+b的值为( )
| A. | 8 | B. | 7 | C. | 15 | D. | 21 |
12.已知二次三项式x2-kx-15能分解成系数为整数的两个一次因式的积,则整数k的取值范围有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.
如图,在正方形ABCD中,P是对角线AC上的一点,点E在BC的延长线上,且PE=PB.