题目内容
7.先化简,再求代数式($\frac{2x}{{x}^{2}-4}-\frac{1}{x+2}$)$÷\frac{x-1}{x-2}$的值,其中x=3tan30°+1.分析 先根据分式混合运算的法则把原式进行化简,再求出x的值代入进行计算即可.
解答 解:原式=[$\frac{2x}{(x+2)(x-2)}$-$\frac{1}{x+2}$]•$\frac{x-2}{x-1}$
=$\frac{x+2}{(x+2)(x-2)}$•$\frac{x-2}{x-1}$
=$\frac{1}{x-1}$,
当x=3tan30°+1=3×$\frac{\sqrt{3}}{3}$+1=$\sqrt{3}$+1时,原式=$\frac{1}{x-1}$=$\frac{1}{\sqrt{3}+1-1}$=$\frac{\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
相关题目
17.若代数式x3+ax2+bx+8其中有两个因式分别为x+1和x+2,则a+b的值为( )
| A. | 8 | B. | 7 | C. | 15 | D. | 21 |
12.已知二次三项式x2-kx-15能分解成系数为整数的两个一次因式的积,则整数k的取值范围有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.以下各式计算正确的是( )
| A. | (y+x)(-y+x)=y2-x2 | B. | -$\root{3}{-{2}^{-3}}$=-2 | C. | (-2a2)3=-8a6 | D. | x6÷x3=x2 |

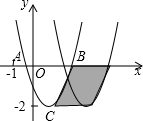 如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论:
如图,已知抛物线y=ax2+bx+c与轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论: