题目内容
7.已知直线y=kx(k≠0)与双曲线$y=\frac{3}{x}$交于点A(x1,y1),B(x2,y2),则x1y2+x2y1的值为-6.分析 由反比例函数与过原点的一次函数的对称性可知“x1=-x2,y1=-y2”,结合反比例函数图象上点的坐标特征可得出“x1•y1=3,x2•y2=3”,由此即可得出结论.
解答 解:∵直线y=kx(k≠0)与双曲线$y=\frac{3}{x}$交于点A(x1,y1),B(x2,y2),
∴x1=-x2,y1=-y2.
∵点A(x1,y1),B(x2,y2)为反比例函数$y=\frac{3}{x}$图象上的点,
∴x1•y1=3,x2•y2=3,
∴x1y2+x2y1=-x1•y1-x2•y2=-3-3=-6.
故答案为:-6.
点评 本题考查了反比例函数与一次函数的交点问题,解题的关键是找出x1=-x2,y1=-y2.本题属于基础题,难度不大,解决该题型题目时,由对称性找出点A、B坐标间的关系,再结合反比例函数图象上点的坐标特征可得出结论.

练习册系列答案
相关题目
12.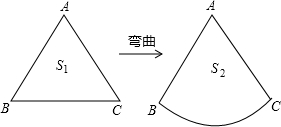 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
 如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )
如图,△ABC为等边三角形,保持各边的长度不变,将BC边向三角形外弯曲得到扇形ABC,设△ABC的面积为S1,扇形ABC的面积为S2,则S1与S2的大小关系为( )| A. | S1<S2 | B. | S1=S2 | C. | S1>S2 | D. | 无法确定 |
 将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.
将一张长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,若这个三角形面积的最小值为4.5cm2时,则纸片的宽为3.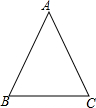 如图,等腰△ABC中,AB=AC.
如图,等腰△ABC中,AB=AC.