题目内容
19.若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点,则有( )| A. | mn≥-9且m≠0,n>0 | B. | -9≤mn≤0 | C. | mn≥-4 | D. | -4≤mn≤0 |
分析 依照题意画出图形,将一次函数解析式代入反比例函数解析式中,得出关于x的一元二次方程,由两者有交点,结合根的判别式即可得出mn≥-9,再根据一次函数的定义以及反比例函数在第一象限有图象,即可得出m≠0,n>0,此题得解.
解答 解:依照题意画出图形,如下图所示.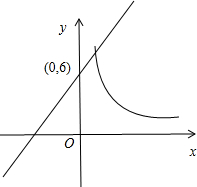
将y=mx+6代入y=$\frac{n}{x}$中,
得:mx+6=$\frac{n}{x}$,整理得:mx2+6x-n=0,
∵二者有交点,
∴△=62+4mn≥0,
∴mn≥-9.
∵y=mx+6为一次函数,反比例函数y=$\frac{n}{x}$在第一象限有图象,
∴m≠0,n>0.
故选A.
点评 本题考查了反比例函数与一次函数的交点问题以及根的判别式,解题的关键由根的判别式得出关于mn的不等式.本题属于基础题,难度不大,解决该题型题目时,画出图形,利用数形结合解决问题是关键.

练习册系列答案
相关题目
9.若$\frac{1}{x+1}$在实数范围内有意义,则x的取值范围是( )
| A. | x≠1 | B. | x>-1 | C. | x≠-1 | D. | x<-1 |
8.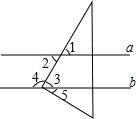 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )| A. | ∠2=60° | B. | ∠3=60° | C. | ∠4=120° | D. | ∠5=40° |
9.已知圆锥的母线长是12,它的侧面展开图的圆心角是120°,则它的底面圆的直径为( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
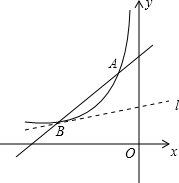 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1).
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1). 如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.
如图,BD是?ABCD的对角线,过点A作AE⊥BD,垂足为E,过点C作CF⊥BD,垂足为F.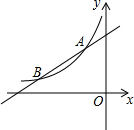 如图,已知一次函数y=$\frac{1}{2}$x+b的图象与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A(-1,2)和点B,点C在y轴上.
如图,已知一次函数y=$\frac{1}{2}$x+b的图象与反比例函数y=$\frac{k}{x}$(x<0)的图象交于点A(-1,2)和点B,点C在y轴上.