题目内容
7．
如图，BD是?ABCD的对角线，过点A作AE⊥BD，垂足为E，过点C作CF⊥BD，垂足为F．（1）补全图形，并标上相应的字母；
（2）求证：AE=CF．
分析 （1）根据题意画出图形即可；
（2）由平行四边形的性质得出△ABD的面积=△BCD的面积，得出$\frac{1}{2}$BD•AE=$\frac{1}{2}$BD•CF，即可得出结论．
解答 （1）解：如图所示：
（2）证明：∵四边形ABCD是平行四边形，
∴△ABD的面积=△BCD的面积，
∴$\frac{1}{2}$BD•AE=$\frac{1}{2}$BD•CF，
∴AE=CF．
点评 本题考查了平行四边形的性质、三角形的面积关系；熟练掌握平行四边形的性质是解决问题的关键．
练习册系列答案
阅读快车系列答案
相关题目
17．关于x的一元二次方程x2-$\sqrt{2}$x+sinα=0有两个相等的实数根，则锐角α等于（ ）
| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
如图，AB为⊙O的直径，F为弦AC的中点，连接OF并延长交$\widehat{AC}$于点D，过点D作⊙O的切线，交BA的延长线于点E．
12．
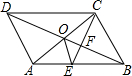如图，?ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC=60°，AB=2BC，连接OE．下列结论：
①∠ACD=30°；②S?ABCD=AC•BC；③OE：AC=$\sqrt{3}$：6；④S△OCF=2S△OEF
成立的个数有（ ）
如图，?ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC=60°，AB=2BC，连接OE．下列结论：①∠ACD=30°；②S?ABCD=AC•BC；③OE：AC=$\sqrt{3}$：6；④S△OCF=2S△OEF
成立的个数有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
19．若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点，则有（ ）
| A． | mn≥-9且m≠0，n＞0 | B． | -9≤mn≤0 | C． | mn≥-4 | D． | -4≤mn≤0 |
16．在平面直角坐标系中，将△AOB绕原点O顺时针旋转180°后得到△A1OB1，若点B的坐标为（2，1），则点B的对应点B1的坐标为（ ）
| A． | （1，2） | B． | （2，-1） | C． | （-2，1） | D． | （-2，-1） |
17．若x0是方程ax2+2x+c=0（a≠0）的一个根，设M=1-ac，N=（ax0+1）2，则M与N的大小关系正确的为（ ）
| A． | M＞N | B． | M=N | C． | M＜N | D． | 不确定 |