题目内容
10.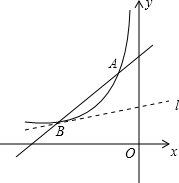 如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1).
如图,一次函数y=x+b的图象与反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象交于点A(-1,4)和点B(a,1).(1)求反比例函数的表达式和a、b的值;
(2)若A、O两点关于直线l对称,请连接AO,并求出直线l与线段AO的交点坐标.
分析 (1)由点A的坐标结合反比例函数图象上点的坐标特征,即可求出k值,从而得出反比例函数解析式;再将点A、B坐标分别代入一次函数y=x+b中得出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)连接AO,设线段AO与直线l相交于点M.由A、O两点关于直线l对称,可得出点M为线段AO的中点,再结合点A、O的坐标即可得出结论.
解答 解:(1)∵点A(-1,4)在反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象上,
∴k=-1×4=-4,
∴反比例函数解析式为y=-$\frac{4}{x}$.
把点A(-1,4)、B(a,1)分别代入y=x+b中,
得:$\left\{\begin{array}{l}{4=-1+b}\\{1=a+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=-4}\\{b=5}\end{array}\right.$.
(2)连接AO,设线段AO与直线l相交于点M,如图所示.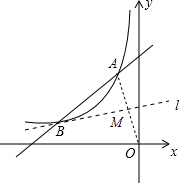
∵A、O两点关于直线l对称,
∴点M为线段OA的中点,
∵点A(-1,4)、O(0,0),
∴点M的坐标为(-$\frac{1}{2}$,2).
∴直线l与线段AO的交点坐标为(-$\frac{1}{2}$,2).
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求函数解析式、解二元一次方程组以及中点坐标公式,解题的关键是:(1)由点的坐标利用待定系数法求函数系数;(2)得出点M为线段AO的中点.本题属于基础题,难度不大,解决该题型题目时,巧妙的利用了中点坐标公式降低了难度.

练习册系列答案
相关题目
1.下列各式计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | x2•x3=x6 | C. | x2+x3=x5 | D. | (a3)3=a9 |
19.若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点,则有( )
| A. | mn≥-9且m≠0,n>0 | B. | -9≤mn≤0 | C. | mn≥-4 | D. | -4≤mn≤0 |
20.化简$\frac{x}{{x}^{2}+2x+1}$$÷(1-\frac{1}{x+1})$的结果是( )
| A. | $\frac{1}{x+1}$ | B. | $\frac{x+1}{x}$ | C. | x+1 | D. | x-1 |
 如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )
如图,是由四个大小相同的小正方体拼成的几何体,则这个几何体的左视图是( )



 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.