题目内容
8.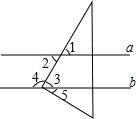 如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )
如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则下列结论错误的是( )| A. | ∠2=60° | B. | ∠3=60° | C. | ∠4=120° | D. | ∠5=40° |
分析 根据平行线的性质:两直线平行,同位角相等,以及对顶角相等等知识分别求出∠2,∠3,∠4,∠5的度数,然后选出错误的选项.
解答 解:∵a∥b,∠1=60°,
∴∠3=∠1=60°,∠2=∠1=60°,
∠4=180°-∠3=180°-60°=120°,
∵三角板为直角三角板,
∴∠5=90°-∠3=90°-60°=30°.
故选D.
点评 本题考查了平行线的性质,解答本题的关键上掌握平行线的性质:两直线平行,同位角相等.

练习册系列答案
相关题目
19.若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点,则有( )
| A. | mn≥-9且m≠0,n>0 | B. | -9≤mn≤0 | C. | mn≥-4 | D. | -4≤mn≤0 |
16.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,-1) |
3.下列四个数中,最小的正数是( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
20.化简$\frac{x}{{x}^{2}+2x+1}$$÷(1-\frac{1}{x+1})$的结果是( )
| A. | $\frac{1}{x+1}$ | B. | $\frac{x+1}{x}$ | C. | x+1 | D. | x-1 |
17.若x0是方程ax2+2x+c=0(a≠0)的一个根,设M=1-ac,N=(ax0+1)2,则M与N的大小关系正确的为( )
| A. | M>N | B. | M=N | C. | M<N | D. | 不确定 |
18.用四舍五入法对3.8963取近似数,精确到0.01,得到的正确结果是( )
| A. | 3.89 | B. | 3.9 | C. | 3.90 | D. | 3.896 |