题目内容
9．已知圆锥的母线长是12，它的侧面展开图的圆心角是120°，则它的底面圆的直径为（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 根据圆锥侧面展开图的圆心角与半径（即圆锥的母线的长度）求得的弧长，就是圆锥的底面的周长，然后根据圆的周长公式l=2πr解出r的值即可．
解答 解：设圆锥的底面半径为r．
圆锥的侧面展开扇形的半径为12，
∵它的侧面展开图的圆心角是120°，
∴弧长=$\frac{120π×12}{180}$=8π，
即圆锥底面的周长是8π，
∴8π=2πr，解得，r=4，
∴底面圆的直径为8．
故选D．
点评 本题考查了圆锥的计算．正确理解圆锥的侧面展开图与原来的扇形之间的关系是解决本题的关键，理解圆锥的母线长是扇形的半径，圆锥的底面圆周长是扇形的弧长．
练习册系列答案
相关题目
19．若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点，则有（ ）
| A． | mn≥-9且m≠0，n＞0 | B． | -9≤mn≤0 | C． | mn≥-4 | D． | -4≤mn≤0 |
20．化简$\frac{x}{{x}^{2}+2x+1}$$÷（1-\frac{1}{x+1}）$的结果是（ ）
| A． | $\frac{1}{x+1}$ | B． | $\frac{x+1}{x}$ | C． | x+1 | D． | x-1 |
17．若x0是方程ax2+2x+c=0（a≠0）的一个根，设M=1-ac，N=（ax0+1）2，则M与N的大小关系正确的为（ ）
| A． | M＞N | B． | M=N | C． | M＜N | D． | 不确定 |
4．
如图，已知∠1=60°，如果CD∥BE，那么∠B的度数为（ ）
如图，已知∠1=60°，如果CD∥BE，那么∠B的度数为（ ）| A． | 70° | B． | 100° | C． | 110° | D． | 120° |
14．
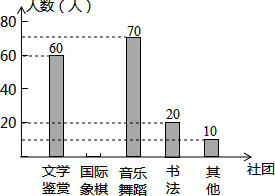为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：
根据统计图表的信息，解答下列问题：
（1）求本次抽样调查的学生总人数及a、b的值；
（2）将条形统计图补充完整；
（3）若该校共有1300名学生，试估计全校选择“音乐舞蹈”社团的学生人数．
为了深化课程改革，某校积极开展校本课程建设，计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团，要求每位学生都自主选择其中一个社团，为此，随机调查了本校部分学生选择社团的意向．并将调查结果绘制成如下统计图表（不完整）：| 选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
| 所占百分比 | a | 20% | b | 10% | 5% |
（1）求本次抽样调查的学生总人数及a、b的值；
（2）将条形统计图补充完整；
（3）若该校共有1300名学生，试估计全校选择“音乐舞蹈”社团的学生人数．
如图，在△ABC中，∠B=60°，AB：AC=5：7，其内切圆⊙O与BC、AC、AB分别切于点D、E、F，且⊙O的面积为12π，求△ABC的三边长．
18．用四舍五入法对3.8963取近似数，精确到0.01，得到的正确结果是（ ）
| A． | 3.89 | B． | 3.9 | C． | 3.90 | D． | 3.896 |
19．在下列图形中，既是轴对称图形，又是中心对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |