题目内容
4.先化简,再求值:($\frac{x}{{x}^{2}+x}$-1)÷$\frac{{x}^{2}-1}{{x}^{2}+2x+1}$,其中x的值从不等式组$\left\{\begin{array}{l}{-x≤1}\\{2x-1<4}\end{array}\right.$的整数解中选取.
分析 先算括号里面的,再算除法,求出x的取值范围,选出合适的x的值代入求值即可.
解答 解:原式=$\frac{x-{x}^{2}-x}{x(x+1)}$•$\frac{x+1}{x-1}$
=-$\frac{x}{x+1}$•$\frac{x+1}{x-1}$
=$\frac{x}{1-x}$,
解不等式组$\left\{\begin{array}{l}-x≤1\\ 2x-1<4\end{array}\right.$得,-1≤x<$\frac{5}{2}$,
当x=2时,原式=$\frac{2}{1-2}$=-2.
点评 本题考查的是分式的化简求值,分式中的一些特殊求值题并非是一味的化简,代入,求值.许多问题还需运用到常见的数学思想,如化归思想(即转化)、整体思想等,了解这些数学解题思想对于解题技巧的丰富与提高有一定帮助.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
14.a,b,c为常数,且(a-c)2>a2+c2,则关于x的方程ax2+bx+c=0根的情况是( )
| A. | 有两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 有一根为0 |
12.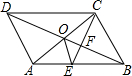 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
 如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
如图,?ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:①∠ACD=30°;②S?ABCD=AC•BC;③OE:AC=$\sqrt{3}$:6;④S△OCF=2S△OEF
成立的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.若一次函数y=mx+6的图象与反比例函数y=$\frac{n}{x}$在第一象限的图象有公共点,则有( )
| A. | mn≥-9且m≠0,n>0 | B. | -9≤mn≤0 | C. | mn≥-4 | D. | -4≤mn≤0 |
9. 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
 如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )
如图,在△ABC中,D、E分别为AB、AC边上的点,DE∥BC,BE与CD相交于点F,则下列结论一定正确的是( )| A. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | B. | $\frac{DF}{FC}=\frac{AE}{EC}$ | C. | $\frac{AD}{DB}=\frac{DE}{BC}$ | D. | $\frac{DF}{BF}=\frac{EF}{FC}$ |
16.在平面直角坐标系中,将△AOB绕原点O顺时针旋转180°后得到△A1OB1,若点B的坐标为(2,1),则点B的对应点B1的坐标为( )
| A. | (1,2) | B. | (2,-1) | C. | (-2,1) | D. | (-2,-1) |
14.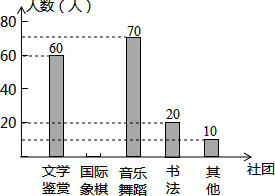 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
 为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等多个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):| 选择意向 | 文学鉴赏 | 国际象棋 | 音乐舞蹈 | 书法 | 其他 |
| 所占百分比 | a | 20% | b | 10% | 5% |
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1300名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
 如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.
如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交$\widehat{AC}$于点D,过点D作⊙O的切线,交BA的延长线于点E.