题目内容
14.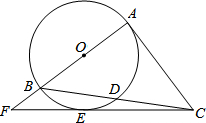 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.(1)求证:CE与⊙O相切;
(2)若⊙O的半径为3,EF=4,求BD的长.
分析 (1)连接OE,OC,通过三角形求得证得∠OEC=∠OAC,从而证得OE⊥CF,即可证得结论;
(2)根据勾股定理求得OF,解直角三角形求得$tanF=\frac{OE}{EF}=\frac{3}{4}$.进而求得AC=6,从而求得△ABC是等腰直角三角形,根据勾股定理求得BC,然后根据等腰三角形三线合一的性质求得DB即可.
解答 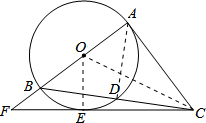 (1)证明:连接OE,OC.
(1)证明:连接OE,OC.
在△OEC与△OAC中,
$\left\{\begin{array}{l}OE=OA\\ OC=OC\\ CE=CA\end{array}\right.$
∴△OEC≌△OAC(SSS),
∴∠OEC=∠OAC.
∵∠OAC=90°,
∴∠OEC=90°.
∴OE⊥CF于E.
∴CF与⊙O相切.
(2)解:连接AD.
∵∠OEC=90°,
∴∠OEF=90°.
∵⊙O的半径为3,
∴OE=OA=3.
在Rt△OEF中,∠OEF=90°,OE=3,EF=4,
∴$OF=\sqrt{O{E^2}+E{F^2}}=5$,$tanF=\frac{OE}{EF}=\frac{3}{4}$.
在Rt△FAC中,∠FAC=90°,AF=AO+OF=8,
∴AC=AF•tanF=6,
∵AB为直径,
∴AB=6=AC,∠ADB=90°.
∴BD=$\frac{BC}{2}$.
在Rt△ABC中,∠BAC=90°,
∴$BC=\sqrt{A{B^2}+A{C^2}}=6\sqrt{2}$.
∴BD=$3\sqrt{2}$.
点评 本题考查了切线的性质,三角形全等的判定和性质,勾股定理的应用,解直角三角形等,作出辅助线构建直角三角形是本题的关键.

练习册系列答案
相关题目
19.对函数y=x3的描述:①y随x的增大而增大,②它的图象是中心对称图形,③它的自变量取值范围是x≠0.正确的是( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
6. 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
3. 如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
 如图,把图形折叠起来,它会变为下面的哪幅立体图形( )
如图,把图形折叠起来,它会变为下面的哪幅立体图形( )| A. |  | B. |  | C. |  | D. |  |
4.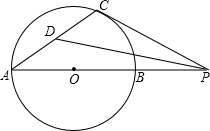 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
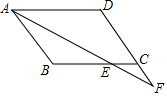 如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.
如图,在四边形ABCD中,AB∥CD,∠BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF,求证:四边形ABCD是平行四边形.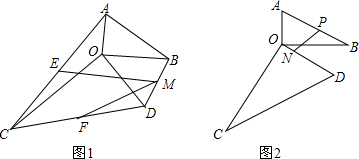
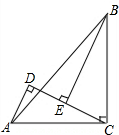 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.