题目内容
6. 如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )
如图,△ABC中,∠C=90°,∠B=60°,AC=2$\sqrt{3}$,点D在AC上,以CD为直径作⊙O与BA相切于点E,则BE的长为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 由∠C=90°,∠B=60°,AC=2$\sqrt{3}$,得到BC=$\frac{AC}{tan60°}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2,由于CD为⊙O直径,得到BC是⊙O的切线,根据切线长定理即可得到结论.
解答 解:∵∠C=90°,∠B=60°,AC=2$\sqrt{3}$,
∴BC=$\frac{AC}{tan60°}$=$\frac{2\sqrt{3}}{\sqrt{3}}$=2,
∵CD为⊙O直径,
∴BC是⊙O的切线,
∴BE=BC=2,
故选C.
点评 本题考查了切线的判定和性质,锐角三角函数,熟记定理是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.两个实根之和为3的一元二次方程是( )
| A. | 2x2-3x+1=0 | B. | x2+1=3x | C. | x2-3x+4=0 | D. | 3x2+9x-1=0 |
17.在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17.2,则四个班体考成绩最稳定的是( )
| A. | 甲班 | B. | 乙班 | C. | 丙班 | D. | 丁班 |
18. 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
15.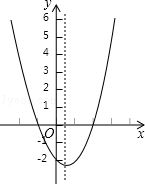 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
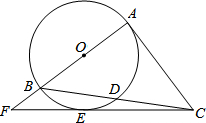 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.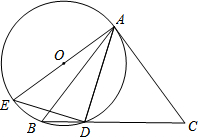 如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.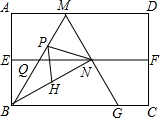 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论: