题目内容
4.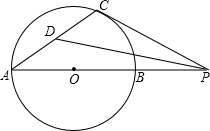 已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )
已知AB是⊙O的直径,点P是AB延长线上的一个动点,过P作⊙O的切线,切点为C,∠APC的平分线交AC于点D.若∠CPD=20°,则∠CAP等于( )| A. | 30° | B. | 20° | C. | 45° | D. | 25° |
分析 连接OC,根据题意,可知OC⊥PC,∠CPD+∠DPA+∠A+∠ACO=90°,可推出∠DPA+∠A=45°,即∠CDP=45°则问题可求.
解答  解:如图,连接OC,
解:如图,连接OC,
∵OC=OA,PD平分∠APC,
∴∠CPD=∠DPA=20°,∠A=∠ACO,
∵PC为⊙O的切线,
∴OC⊥PC,
∵∠CPO+∠COP=90°,
∴(∠CPD+∠DPA)+(∠A+∠ACO)=90°,
∴∠DPA+∠A=45°,
∴∠CDP=45°,
∴∠CAP=25°.
故选D.
点评 本题主要考查了切线的性质、等边三角形的性质、角平分线的性质、外角的性质,解题的关键在于作好辅助线构建直角三角形.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
15.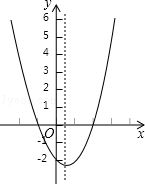 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
13.下列计算,正确的是( )
| A. | x3•x4=x12 | B. | (x3)3=x6 | C. | (3x)2=9x2 | D. | 2x2÷x=x |
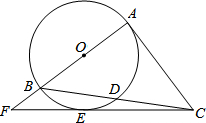 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.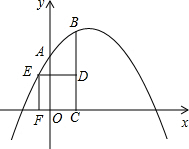 如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.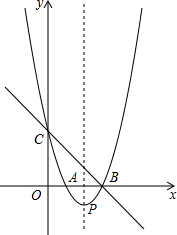 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.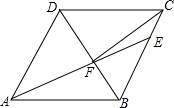 如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为$\frac{12}{5}$$\sqrt{3}$.其中一定成立的是①②③(把所有正确结论的序号都填在横线上).
如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,CE=2,连接CF,以下结论:①△ABF≌△CBF;②点E到AB的距离是2$\sqrt{3}$;③tan∠DCF=$\frac{3\sqrt{3}}{7}$;④△ABF的面积为$\frac{12}{5}$$\sqrt{3}$.其中一定成立的是①②③(把所有正确结论的序号都填在横线上).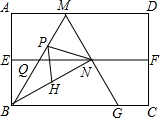 如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论: