题目内容
9.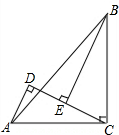 已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.
已知:如图,在△ABC中,∠ACB=90°,AC=BC,BE⊥CE于点E,AD⊥CE于点D.求证:BE=CD.
分析 根据垂直的定义以及等量代换可知∠CBE=∠ACD,根据已知条件∠BEC=∠CDA,∠CBE=∠ACD,BC=AC,根据全等三角形的判定AAS即可证明△BEC≌△CDA,再利用全等三角形的性质证明即可.
解答 证明:∵BE⊥CE,AD⊥CE,
∴∠BEC=∠CDA=90°,
∴∠EBC+∠ECB=90°,
又∵∠DCA+∠ECB=90°,
∴∠EBC=∠DCA,
又∵BC=AC,
在△BEC与△CDA中,
$\left\{\begin{array}{l}{∠BEC=∠CDA}\\{∠CBE=∠ACD}\\{BC=AC}\end{array}\right.$,
∴△BEC≌△CDA(AAS),
∴BE=CD.
点评 本题考查了全等三角形的判定定理,关键是根据AAS证明两三角形全等,难度适中.

练习册系列答案
相关题目
17.在今年的中招体育考试中,我校甲、乙、丙、丁四个班级的平均分完全一样,方差分别为:S甲2=8.5,S乙2=21.7,S丙2=15,S丁2=17.2,则四个班体考成绩最稳定的是( )
| A. | 甲班 | B. | 乙班 | C. | 丙班 | D. | 丁班 |
4.学习了一次函数、二次函数、反比例函数后,爱钻研的小敏尝试用同样的方法研究函数y=$\frac{3x+1}{x}$并作了三个推测:
(1)当x>0时,y的值随着x的增大越来越小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近于3.
则推测正确的是( )
(1)当x>0时,y的值随着x的增大越来越小;
(2)y的值有可能等于3;
(3)当x>0时,y的值随着x的增大越来越接近于3.
则推测正确的是( )
| A. | (1)(2) | B. | (1)(3) | C. | (2)(3) | D. | (1)(2)(3) |
18. 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
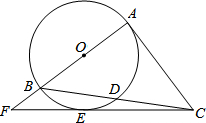 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F. 如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.
如图,∠1=70°,直线a平移后得到直线b,则∠2-∠3=110°.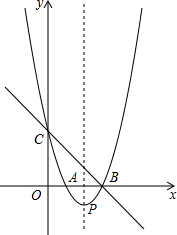 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.