题目内容
2.已知两个以O为顶点且不全等的直角三角形△AOB和△COD,其中∠ABO=∠DCO=30°.(1)如图1,设∠BOD=α(0°<α<60°),点E、F、M分别是AC、CD、DB的中点.连接FM、EM.请问:随着α的变化,试判断$\frac{FM}{EM}$的值是否发生变化?若不变,请求出$\frac{FM}{EM}$的值;若变化,请说明理由;
(2)如图2,若BO=3,点N在线段OD上,且NO=1,点P是线段AB上的一个动点,将△COD固定,△AOB绕点O旋转的过程中,线段PN长度的最大值是4;最小值是$\frac{1}{2}$.
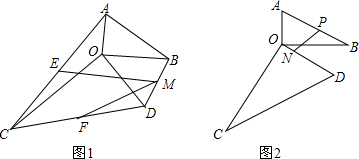
分析 (1)连接AD、BC,由∠AOB=∠COD=90°∠ABO=∠DCO=30°,得到$\frac{OA}{OB}=\frac{OD}{OC}=\frac{\sqrt{3}}{3}$,∠AOD=∠BOC,推出△AOD∽△BOC,求得∠OAD=∠CBO,$\frac{AD}{BC}=\frac{\sqrt{3}}{3}$,证得AD⊥BC由于点E、F、M分别是AC、CD、DB的中点,根据三角形的中位线的性质得到EF∥AD,EF=$\frac{1}{2}$AD,于是得到MF∥AD,MF=$\frac{1}{2}$AD,在Rt△EFM中,$\frac{FM}{EM}$=$\frac{\sqrt{3}}{2}$;
(2)过O作OE⊥AB于E,由已知条件求出当P在点E处时,点P到O点的距离最近为$\frac{3}{2}$,当旋转到OE与OD重合是,NP取最小值为:OP-ON=$\frac{1}{2}$;当点P在点B处时,且当旋转到OB在DO的延长线时,NP取最大值OB+ON=4.
解答 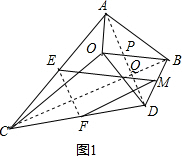 解:(1)不变;$\frac{FM}{EM}$=$\frac{\sqrt{3}}{2}$,
解:(1)不变;$\frac{FM}{EM}$=$\frac{\sqrt{3}}{2}$,
如图1,连接AD、BC交于一点Q,AD交BO于P,
∵∠AOB=∠COD=90°,
∠ABO=∠DCO=30°,
∵$\frac{OA}{OB}=\frac{OD}{OC}=\frac{\sqrt{3}}{3}$,∠AOD=∠BOC,
∴△AOD∽△BOC,
∴∠OAD=∠CBO,$\frac{AD}{BC}=\frac{\sqrt{3}}{3}$,
∵∠APO=∠BPQ,
∴∠BQP=∠AOB=90°,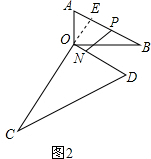 ∴AD⊥BC,
∴AD⊥BC,
∵点E、F、M分别是AC、CD、DB的中点,
∴EF∥AD,EF=$\frac{1}{2}$AD,
∴MF∥BC,MF=$\frac{1}{2}$BC,
在Rt△EFM中,$\frac{FM}{EM}$=$\frac{\sqrt{3}}{2}$;
(2)如图2,过O作OE⊥AB于E,
∵BO=3,∠ABO=30°,
∴AO=$\frac{\sqrt{3}}{3}$,AB=$\frac{2\sqrt{3}}{3}$,
∴$\frac{1}{2}$AB•OE=$\frac{1}{2}$OA•OB,
∴OE=$\frac{3}{2}$,
∴当P在点E处时,点P到O点的距离最近为$\frac{3}{2}$,
这时当旋转到OE与OD重合是,NP取最小值为:OP-ON=$\frac{1}{2}$;
如图4,当点P在点B处时,且当旋转到OB在DO的延长线时,NP取最大值OB+ON=3+1=4,
∴线段PN长度的最小值为$\frac{1}{2}$,最大值为4.
故答案为:4,$\frac{1}{2}$.
点评 此题考查了旋转的性质、相似三角形的判定与性质、直角三角形的判定和性质三角形的中位线的判定和性质、三角函数的应用.此题难度较大,注意数形结合思想的应用,注意旋转前后的对应关系.

| A. |  | B. |  | C. |  | D. |  |
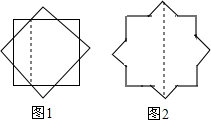 如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.
如图2的正八角形是由两个正方形(如图1)中的一个正方形绕着它的中心顺时针旋转45°形成的.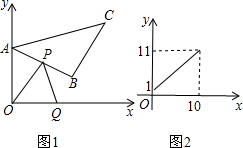
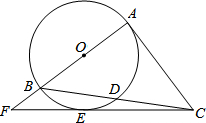 如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.
如图,Rt△ABC中,∠A=90°,以AB为直径的⊙O交BC于点D,点E在⊙O上,CE=CA,AB,CE的延长线交于点F.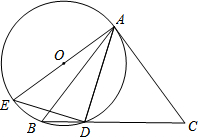 如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.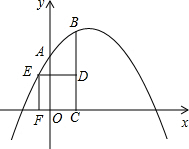 如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.
如图,抛物线y=-$\frac{1}{2}$x2+bx+c过A(0,2),B(1,3),CB⊥x轴于点C,四边形CDEF为正方形,点D在线段BC上,点E在此抛物线上,且在直线BC的左侧,则正方形CDEF的边长为$\frac{-3+\sqrt{33}}{2}$.