题目内容
1.某商场购进商品后,加价40%作为销售价.商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,两种商品原售价之和为490元,甲、乙两种商品的进价分别是( )| A. | 200元,150元 | B. | 210元,280元 | C. | 280元,210元 | D. | 150元,200元 |
分析 设甲种商品的进价为x元,乙种商品的进价为y元,结合“购进商品后加价40%作为销售价.商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,两种商品原售价之和为490元”列出方程组并解答.
解答 解:设甲种商品的进价为x元,乙种商品的进价为y元,
依题意得:$\left\{\begin{array}{l}{(1+40%)x+(1+40%)y=490}\\{(1+40%)x•0.7+(1+40%)y•0.9=399}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=150}\\{y=200}\end{array}\right.$,
故选:D.
点评 本题考查二元一次方程组的应用,需要学生具备理解题意的能力,根据销售价格和打折后的价格可列方程组求解.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
17.化简($\sqrt{3}$-2)200•($\sqrt{3}+2$)201的结果为( )
| A. | -1 | B. | $\sqrt{3}$-2 | C. | $\sqrt{3}$+2 | D. | -$\sqrt{3}$-2 |
18.如果(x2-mx-n)(x-3)的乘积中不含x2项和x项,那么( )
| A. | m=0,n=0 | B. | m=-3,n=-9 | C. | m=-3,n=9 | D. | m=3,n=-9 |
15.设ab≠0,a2+b2=1,如果x=$\frac{{a}^{4}+{b}^{4}}{{a}^{6}+{b}^{6}}$,y=$\frac{{a}^{4}+{b}^{4}}{\sqrt{{a}^{4}+{b}^{4}}}$,z=$\frac{\sqrt{{a}^{4}+{b}^{4}}}{{a}^{6}+{b}^{6}}$,那么x,y,z的大小关系是( )
| A. | x<y<z | B. | y<z<x | C. | z<x<y | D. | y<x<z |
10.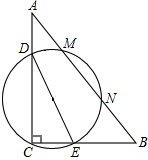 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
 如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )
如图,在直角△ABC中,∠C=90°,BC=3,AC=4,D、E分别是AC、BC上的一点,且DE=3.若以DE为直径的圆与斜边AB相交于M、N,则MN的最大值为( )| A. | $\frac{8}{5}$ | B. | 2 | C. | $\frac{12}{5}$ | D. | $\frac{14}{5}$ |

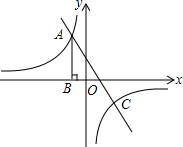 如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4.
如图,反比例函数y=$\frac{k}{x}$的图象经过第二象限内的点A,AB⊥x轴于点B,OB=1,AB=4. 如图,直线y=kx(k>0)与双轴线y=$\frac{3}{x}$相交于A,B两点,作AC⊥x轴,垂足为C,连接BC,则△ABC的面积是3.
如图,直线y=kx(k>0)与双轴线y=$\frac{3}{x}$相交于A,B两点,作AC⊥x轴,垂足为C,连接BC,则△ABC的面积是3.