题目内容
3. 如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.
如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.(1)试判断BF与BG之间的数量关系,并说明理由;
(2)求∠FBG的度数.
分析 (1)根据SAS证明△ABG≌△CFB,再利用全等三角形的性质证明即可;
(2)根据全等三角形的性质得出∠G=∠FBD,再证明即可.
解答 解:(1)BF=BG;
∵AD,CE是高,
∴∠BAD+∠AFE=∠BCF+∠CFD=90°,
∵∠AFE=∠CFD,
∴∠BAD=∠BCF,
在△ABG与△CFB中,
$\left\{\begin{array}{l}{AG=BC}\\{∠BAD=∠BCF}\\{CF=AB}\end{array}\right.$,
∴△ABG≌△CFB,
∴BF=BG;
(2)∵△ABG≌△CFB,
∴∠G=∠FBD,
∵∠FBD+∠DBG=90°,
∴∠G+∠DBG=90°,
∴∠FBG的度数为90°.
点评 此题考查全等三角形的判定和性质,关键是根据SAS证明△ABG≌△CFB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.若二次函数y=ax2+bx+c(a≠0)的图象与x轴有两个不同的交点,坐标分别为(x1,0),(x2,0),且x1<x2,图象上有一点M (x0,y0)在x轴下方,则下列判断正确的是( )
| A. | a>0 | B. | a(x0-x1)( x0-x2)<0 | C. | x1<x0<x2 | D. | b2-4ac≥0 |
8.一元二次方程x2-4x+3=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 不能确定 |
15.若等腰三角形中相等的两边的长为10cm,第三边长为16cm,则第三边的高为( )
| A. | 12cm | B. | 10cm | C. | 8cm | D. | 6cm |
12. 如图,△ABC≌△ADE,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
如图,△ABC≌△ADE,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
 如图,△ABC≌△ADE,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )
如图,△ABC≌△ADE,点D落在BC上,且∠B=60°,则∠EDC的度数等于( )| A. | 45° | B. | 30° | C. | 60° | D. | 75° |
 如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是35°.
如图,AB是半圆的直径,∠BAC=20°,D是$\widehat{AC}$的中点,则∠DAC的度数是35°.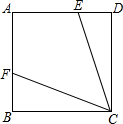 如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( )
如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( ) 如图所示,AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,AB的长为8cm.
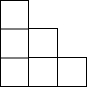
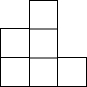
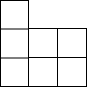
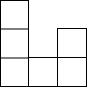
如图所示,AB比AC长2cm,BC的垂直平分线交AB于D,交BC于E,△ACD的周长是14cm,AB的长为8cm.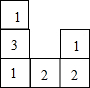 右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的主视图是( )
右图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何体的主视图是( )