题目内容
11.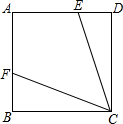 如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( )
如图,在正方形ABCD中,BC=5,点E、F分别在AD,AB上,连接CE,CF.若AF=3,∠AFC=∠D+∠DCE,则△CDE的面积为( )| A. | 15 | B. | 10 | C. | 7.5 | D. | 5 |
分析 由正方形的性质得出AB=CD=AD=BC=5,∠B=∠D=90°,由三角形的外角性质和已知条件得出∠BCF=∠DCE,由ASA证明△BCF≌△DCE,得出DE=BF=AB-AF=2,即可求出△CDE的面积.
解答 解:∵四边形ABCD是正方形,
∴AB=CD=AD=BC=5,∠B=∠D=90°,
∵∠AFC=∠B+∠BCF,∠AFC=∠D+∠DCE,
∴∠BCF=∠DCE,
在△BCF和△DCE中,
$\left\{\begin{array}{l}{∠B=∠D}&{\;}\\{BC=DC}&{\;}\\{∠BCF=∠DCE}&{\;}\end{array}\right.$,
∴△BCF≌△DCE(ASA),
∴DE=BF=AB-AF=2,
∴△CDE的面积=$\frac{1}{2}$CD•DE=$\frac{1}{2}$×5×2=5.
故选:D.
点评 本题考查了正方形的性质、全等三角形的判定与性质、三角形面积的计算方法;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
2. 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2,
其中说法正确的是( )
 如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:
如图,二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x=$\frac{1}{2}$,且经过点(2,0),下列说法:①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(-2,y1),(-3,y2)是抛物线上的两点,则y1<y2,
其中说法正确的是( )
| A. | ①②④ | B. | ③④ | C. | ①③④ | D. | ①② |
6.解分式方程$\frac{1}{2x-3}$-4=$\frac{5}{3-2x}$时,去分母后可得( )
| A. | 1-4(2x-3)=-5 | B. | 1-4(2x-3)=5 | C. | 2x-3-4=-5 | D. | 2x-3-4=5(2x-3) |
16.2015年9月6日河北新闻网报道,2011-2014年,河北省共争取中央扶贫发展资金35.9亿元,省本级累计安排专项扶贫资金27.85亿元,27.85用四舍五入法精确到十分位的结果是( )
| A. | 27 | B. | 27.8 | C. | 27.9 | D. | 27.85 |
 如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.
如图,在△ABC中,AD,CE是高,AD与CE交于点F,连接BF,延长AD到点G,使得AG=BC,连接BG,若CF=AB.