题目内容
13．若二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个不同的交点，坐标分别为（x1，0），（x2，0），且x1＜x2，图象上有一点M （x0，y0）在x轴下方，则下列判断正确的是（ ）| A． | a＞0 | B． | a（x0-x1）（ x0-x2）＜0 | C． | x1＜x0＜x2 | D． | b2-4ac≥0 |
分析 根据抛物线与x轴有两个不同的交点，根的判别式△＞0，再分a＞0和a＜0两种情况对C、D选项讨论即可得解．
解答 解：A、二次函数y=ax2+bx+c（a≠0）的图象与x轴有两个交点无法确定a的正负情况，故本选项错误；
B、若a＞0，则x0-x1＞0，x0-x2＜0，
∴（x0-x1）（x0-x2）＜0．
∴a（x0-x1）（x0-x2）＜0．
若a＜0，则（x0-x1）与（x0-x2）同号，
∴a（x0-x1）（x0-x2）＜0．
综上所述，a（x0-x1）（x0-x2）＜0正确，故本选项正确；
C、若a＞0，则x1＜x0＜x2，
若a＜0，则x0＜x1＜x2或x1＜x2＜x0，故本选项错误；
D、∵x1＜x2，
∴△=b2-4ac＞0，故本选项错误．
故选：B．
点评 本题考查了二次函数与x轴的交点问题，熟练掌握二次函数图象以及图象上点的坐标特征是解题的关键，B、C选项要注意分情况讨论．
练习册系列答案
相关题目
5．
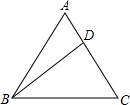如图，在△ABC中，AB=AC=10，BC=12，有一点D在AC上移动，则AD+BD+CD的最小值是（ ）
如图，在△ABC中，AB=AC=10，BC=12，有一点D在AC上移动，则AD+BD+CD的最小值是（ ）| A． | 18 | B． | 18.6 | C． | 20 | D． | 19.6 |
如图，二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x=$\frac{1}{2}$，且经过点（2，0），下列说法：
如图，在△ABC中，AD，CE是高，AD与CE交于点F，连接BF，延长AD到点G，使得AG=BC，连接BG，若CF=AB．