题目内容
14．
如图，AB是半圆的直径，∠BAC=20°，D是$\widehat{AC}$的中点，则∠DAC的度数是35°．
分析 首先连接BC，由AB是半圆的直径，根据直径所对的圆周角是直角，可得∠C=90°，继而求得∠B的度数，然后由D是$\widehat{AC}$的中点，根据弧与圆周角的关系，即可求得答案．
解答 
解：连接BC，
∵AB是半圆的直径，
∴∠C=90°，
∵∠BAC=20°，
∴∠B=90°-∠BAC=70°，
∵D是$\widehat{AC}$的中点，
∴∠DAC=$\frac{1}{2}$∠B=35°．
故答案为：35°．
点评 此题考查了圆周角定理．注意准确作出辅助线是解此题的关键．
练习册系列答案
相关题目
5．
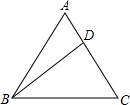如图，在△ABC中，AB=AC=10，BC=12，有一点D在AC上移动，则AD+BD+CD的最小值是（ ）
如图，在△ABC中，AB=AC=10，BC=12，有一点D在AC上移动，则AD+BD+CD的最小值是（ ）| A． | 18 | B． | 18.6 | C． | 20 | D． | 19.6 |
2．
如图，二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x=$\frac{1}{2}$，且经过点（2，0），下列说法：
①abc＜0；
②a+b=0；
③4a+2b+c＜0；
④若（-2，y1），（-3，y2）是抛物线上的两点，则y1＜y2，
其中说法正确的是（ ）
如图，二次函数y=ax2+bx+c（a≠0）图象的一部分，对称轴为直线x=$\frac{1}{2}$，且经过点（2，0），下列说法：①abc＜0；
②a+b=0；
③4a+2b+c＜0；
④若（-2，y1），（-3，y2）是抛物线上的两点，则y1＜y2，
其中说法正确的是（ ）
| A． | ①②④ | B． | ③④ | C． | ①③④ | D． | ①② |
6．解分式方程$\frac{1}{2x-3}$-4=$\frac{5}{3-2x}$时，去分母后可得（ ）
| A． | 1-4（2x-3）=-5 | B． | 1-4（2x-3）=5 | C． | 2x-3-4=-5 | D． | 2x-3-4=5（2x-3） |
如图，在△ABC中，AD，CE是高，AD与CE交于点F，连接BF，延长AD到点G，使得AG=BC，连接BG，若CF=AB．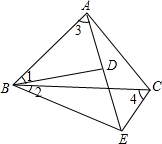
如图，∠1=∠2，∠3=∠4，试问：BD•AC=AB•DE成立吗？说说你的理由．