题目内容
7. 已知:如图所示,圆锥的母线SA=6cm,底面直径AB=4cm,点P是母线SB上一动点(不与点S重合),一只小蚂蚁从点A出发,经过点P绕侧面一周再回到点A处,当点P距离点B3cm时,小蚂蚁行走的路线最短.
已知:如图所示,圆锥的母线SA=6cm,底面直径AB=4cm,点P是母线SB上一动点(不与点S重合),一只小蚂蚁从点A出发,经过点P绕侧面一周再回到点A处,当点P距离点B3cm时,小蚂蚁行走的路线最短.
分析 根据题意得当AP⊥SB时,小蚂蚁行走的路线最短,根据弧长的公司得到∠ASA′=120°,解直角三角形得到BP=3cm,于是得到结论.
解答  解:如图,圆锥的侧面展开图如图所示,
解:如图,圆锥的侧面展开图如图所示,
当AP⊥SB时,小蚂蚁行走的路线最短,
∵SA=6cm,底面直径AB=4cm,
设∠ASA′=n,
∴$\frac{n•π×6}{180}$=4π,
∴n=120°,
∴∠ASA′=120°,
∴∠ASB=60°,
∴SP=$\frac{1}{2}$AS=3cm,
∴BP=3cm,
∴当点P距离点B3cm时,小蚂蚁行走的路线最短.
故答案为:3.
点评 本题考查了圆锥的计算,平面展开-最短距离问题,正确的作出图形是解题的关键.

练习册系列答案
相关题目
17.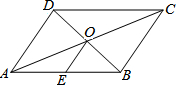 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
 如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )
如图,?ABCD中,对角线AC、BD交于点O,点E是AB的中点.若OE=3cm,则BC的长为( )| A. | 3cm | B. | 6cm | C. | 9cm | D. | 12cm |
18.不等式组$\left\{\begin{array}{l}2x-1>0\\ \frac{1}{2}(x+4)≤3.\end{array}\right.$的解集是$\frac{1}{2}$<x≤2.
2. 在A、B、C内分别填上适当的数,使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C的三数依次是( )
在A、B、C内分别填上适当的数,使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C的三数依次是( )
 在A、B、C内分别填上适当的数,使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C的三数依次是( )
在A、B、C内分别填上适当的数,使得它们折成正方体后,对面上的数互为倒数,则填入正方形A、B、C的三数依次是( )| A. | $\frac{1}{2},\frac{1}{3},1$ | B. | $\frac{1}{3},\frac{1}{2},1$ | C. | $1,\frac{1}{3},\frac{1}{2}$ | D. | $\frac{1}{2},1,\frac{1}{3}$ |
12. 如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
 如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )
如图所示,△DEF是△ABC沿水平方向向右平移后的对应图形,若∠B=31°,∠C=79°,则∠D的度数是( )| A. | 70° | B. | 31° | C. | 79° | D. | 90° |