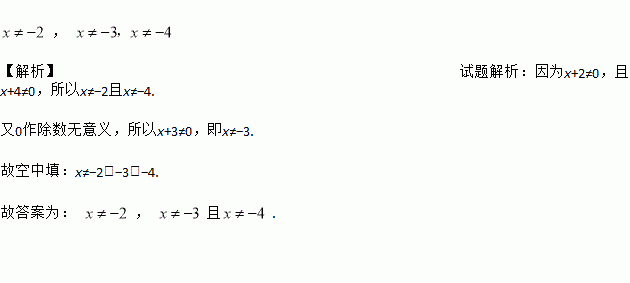题目内容
若代数式 有意义,则x的取值范围是________
有意义,则x的取值范围是________
 ,
【解析】试题解析:因为x+2≠0,且x+4≠0,所以x≠?2且x≠?4.
又0作除数无意义,所以x+3≠0,即x≠?3.
故空中填:x≠?2,?3,?4.
故答案为: , 且.
,
【解析】试题解析:因为x+2≠0,且x+4≠0,所以x≠?2且x≠?4.
又0作除数无意义,所以x+3≠0,即x≠?3.
故空中填:x≠?2,?3,?4.
故答案为: , 且.
练习册系列答案
相关题目
如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
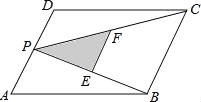
A.24 B.12 C.6 D.3
 B
【解析】
试题分析:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S...
B
【解析】
试题分析:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S... 公路全长为skm,骑自行车t小时可到达,为了提前半小时到达,骑自行车每小时应多走_____________.
 -
【解析】公路全长为skm,骑自行车t小时可到达,则速度为 若提前半小时到达,则速度为 则现在每小时应多走( )
-
【解析】公路全长为skm,骑自行车t小时可到达,则速度为 若提前半小时到达,则速度为 则现在每小时应多走( ) 已知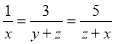 ,则
,则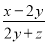 的值为( )
的值为( )
A. 1 B. 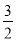 C.
C. 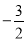 D.
D. 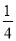
 B
【解析】令,= ,则 则= .
故选B.
B
【解析】令,= ,则 则= .
故选B. 先化简,再求值:  ,其中a= -
,其中a= -
 9
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
当时,原式
9
【解析】试题分析:按照分式混合运算的顺序进行运算即可.
试题解析:
当时,原式 下列各式的计算结果中,是分式的是( )
①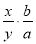 ;②
;②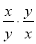 ③
③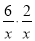 ④
④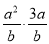 .
.
A. ① B. ①④ C. ②④ D. ①③④
 D
【解析】试题解析:①结果是分式.
②结果不是分式.
③结果是分式.
④结果是分式.
故选D.
D
【解析】试题解析:①结果是分式.
②结果不是分式.
③结果是分式.
④结果是分式.
故选D. 小明解方程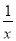 -
-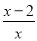 =1的过程如下:
=1的过程如下:
【解析】
方程两边乘x,得1-(x-2)=1.①
去括号,得1-x-2=1.②
移项,得-x=1-1+2.③
合并同类项,得-x=2.④
解得x=-2.⑤
所以,原分式方程的解为x=-2.⑥
请指出他解答过程中的错误,并写出正确的解答过程.
 见解析
【解析】试题分析:去分母时,注意是否每一项都乘以x,去括号,移项时,注意符合的变化;最后注意分式方程一定要检验方程的解。
【解析】
小明的解法有三处错误,步骤①去分母有误; 步骤②去括号有误;步骤⑥少检验.
正确解法为:方程两边乘x,得1-(x-2)=x.
去括号,得1-x+2=x.
移项,得-x-x=-1-2.
合并同类项,得-2x=-3.
解...
见解析
【解析】试题分析:去分母时,注意是否每一项都乘以x,去括号,移项时,注意符合的变化;最后注意分式方程一定要检验方程的解。
【解析】
小明的解法有三处错误,步骤①去分母有误; 步骤②去括号有误;步骤⑥少检验.
正确解法为:方程两边乘x,得1-(x-2)=x.
去括号,得1-x+2=x.
移项,得-x-x=-1-2.
合并同类项,得-2x=-3.
解... 下列各式: 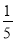 (1?– x),
(1?– x),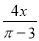 ,
, 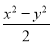 ,
, 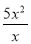 ,其中分式有( )
,其中分式有( )
A. 1个 B. 2个 C. 3个 D. 4个
 A
【解析】是分式;
(1?– x),, 是整式;
故选A.
A
【解析】是分式;
(1?– x),, 是整式;
故选A. 若分式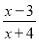 的值为0,则x的值是( )
的值为0,则x的值是( )
A. 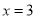 B.
B. 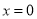 C.
C. 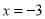 D.
D. 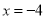
 A
【解析】根据题意可得: =0,方程两边同时乘以(x+4)得:x-3=0,解得:x=3;检验:将x=3代入x+4=7≠0,故x=3为原方程的解。
故本题正确答案为A。
A
【解析】根据题意可得: =0,方程两边同时乘以(x+4)得:x-3=0,解得:x=3;检验:将x=3代入x+4=7≠0,故x=3为原方程的解。
故本题正确答案为A。