题目内容
如图，P为平行四边形ABCD的边AD上的一点，E，F分别为PB，PC的中点，△PEF，△PDC，△PAB的面积分别为S，S1，S2．若S=3，则S1+S2的值为（ ）
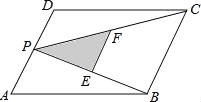
A．24 B．12 C．6 D．3
B
【解析】
试题分析：过P作PQ∥DC交BC于点Q，由DC∥AB，得到PQ∥AB，
∴四边形PQCD与四边形APQB都为平行四边形，
∴△PDC≌△CQP，△ABP≌△QPB，
∴S△PDC=S△CQP，S△ABP=S△QPB，
∵EF为△PCB的中位线，
∴EF∥BC，EF=BC，
∴△PEF∽△PBC，且相似比为1：2，
∴S△PEF：S...
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如果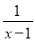
与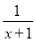
互为相反数，则x＝______．
0
【解析】由题意得+=0，
解得：x=0，
经检验x=0是原方程的解，
故答案为：0. 如图，C、D分别是一个湖的南、北两端A和B正东方向的两个村庄，CD=6km，且D位于C的北偏东30°方向上，则AB的长为（ ）
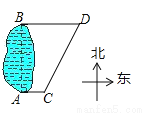
A. 2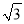
km B. 3
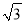km C.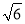 
km D. 3km
B
【解析】试题分析：过点C作CE⊥BD，则∠DCE=30°，根据CD=6km可得：CE=3km，故AB=CE=3km，故选B． 如图，□ABCD的周长为16 cm，AC，BD相交于点O，EO⊥BD交AD于点E，则△ABE的周长为( )
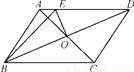
A. 4 cm B. 6 cm C. 8 cm D. 10 cm
C
【解析】试题解析：∵四边形ABCD是平行四边形，
∴AB=DC，AD=BC，BO=DO，
∵EO⊥BO，
∴BE=DE，
故选C. 如图，?ABCD中，BC=BD，∠C=74°，则∠ADB的度数是（ ）
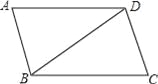
A. 16° B. 22° C. 32° D. 68°
C
【解析】试题分析：根据平行四边形的性质可知：AD∥BC，所以∠C+∠ADC=180°，再由BC=BD可得∠C=∠BDC=74°，进而可求出∠ADB=106°﹣74°=32°．
故选：C． n边形的外角和与内角和的度数之比为2:7,则边数为______
9
【解析】由题意得：
（n-2）•180°：360°=7：2，
解得n=9，
故答案为：9． 内角和等于外角和2倍的多边形是（ ）
A. 五边形 B. 六边形 C. 七边形 D. 八边形
B
【解析】试题分析：本题应先设这个多边形的边数为n，则依题意可列出方程（n﹣2）×180°=360°×2，从而解出n=6，即这个多边形的边数为6．
【解析】
设这个多边形的边数为n，则依题意可得：
（n﹣2）×180°=360°×2，
解得n=6，
∴这个多边形的边数为6．
故选B． 观察下列各式：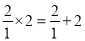 
， 
； 
； 
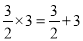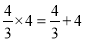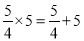；…想一想，什么样的两数之积等于这两数之和？设n表示正整数，用关于n的等式表示这个规律为________________.
【解析】根据一系列的等式，发现：满足 的两个数的积等于它们的和(n表示正整数). 用关于n的等式表示这个规律为.
故答案： . 若代数式
有意义，则x的取值范围是________
，
【解析】试题解析：因为x+2≠0，且x+4≠0，所以x≠?2且x≠?4.
又0作除数无意义，所以x+3≠0，即x≠?3.
故空中填：x≠?2，?3，?4.
故答案为： ， 且.