题目内容
11.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如表:| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(2)要使所获利润不超过进货价格的40%,则A型文具至少买多少只?
(3)在(2)的条件下,应如何选购文具使销售文具所获利润最大?最大利润是多少?
分析 (1)设A文具为x只,则B文具为(100-x)只,根据题意列出方程,解方程解答即可;
(2)设A文具为x只,则B文具为(100-x)只,根据题意列出不等式,解不等式解答即可;
(3)根据一次函数的性质:k<0时,y随x的增大而减小解答即可.
解答 解:(1)设A文具为x只,则B文具为(100-x)只,可得:
10x+15(100-x)=1300,
解得:x=40,
100-x=60,
答:A文具为40只,B文具为60只;
(2)设A文具为x只,则B文具为(100-x)只,可得
(12-10)x+(23-15)(100-x)≤40%[10x+15(100-x)],
解得:x≥50,
答:要使所获利润不超过进货价格的40%,则A型文具至少买50只;
(3)设利润为y,则可得:y=(12-10)x+(23-15)(100-x)=2x+800-8x=-6x+800,
∵k=-6<0,
∴y随x的增大而减小,
所以当x=50时,利润最大,即最大利润=-50×6+800=500元.
点评 本题考查的是一次函数的应用,关键是根据题意列出方程和不等式,解答时,注意一次函数的性质的灵活运用.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案
相关题目
9. 如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
 如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )
如图,四边形ABCD是正方形,点E、F分别在线段BC、DC上线段AE绕点A逆时针旋转后与线段AF重合.若∠BAE=40°,则旋转的角度是( )| A. | 10° | B. | 15° | C. | 40° | D. | 50° |
10.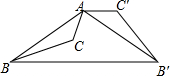 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
16.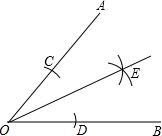 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE是∠AOB的平分线 | B. | OC=OD | ||
| C. | 点C、D到OE的距离不相等 | D. | ∠AOE=∠BOE |
3. 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
 如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )
如图所示,已知线段MN,若用尺规作图作出MN的中点O,然后再取OM的中点A,然后分别以O、A为圆心,以OM长为半径画弧,两弧交于点B,测量∠MBN的度数,结果为( )| A. | 70° | B. | 80° | C. | 90° | D. | 100° |
 如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=$\frac{1}{2}BC$.
如图,在△ABC中,AB=AC,AD是BC边上的中线,AE⊥BE于点E,且BE=$\frac{1}{2}BC$.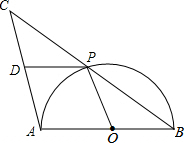 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.