题目内容
20.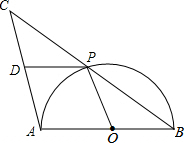 如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.
如图,AB是半圆O的直径,点P是半圆上不与点A、B重合的一个动点,延长BP到点C,使PC=PB,D是AC的中点,连接PD、PO.(1)求证:四边形ADPO是菱形;
(2)求证:△CDP≌△POB.
分析 (1)根据三角形中位线定理得出DP∥AB,DP=$\frac{1}{2}$AB,再由OA=OB可知DP=OA,故四边形AOPD是平行四边形,根据OP=OA可得出结论;
(2)根据中位线的性质得到DP∥AB,DP=$\frac{1}{2}$AB,由SAS可证△CDP≌△POB.
解答 (1)证明:∵PC=PB,D是AC的中点,
∴DP是△ABC的中位线,
∴DP∥AB,DP=$\frac{1}{2}$AB.
∵OA=OB,
∴DP=OA,
故四边形AOPD是平行四边形.
∵OP=OA,
∴四边形ADPO是菱形;
(2)证明:∵PC=PB,D是AC的中点,
∴DP∥AB,
∴DP=$\frac{1}{2}$AB,∠CPD=∠PBO,
∵BO=$\frac{1}{2}$AB,
∴DP=BO,
在△CDP与△POB中,
∵$\left\{\begin{array}{l}DP=BO\\∠CPD=∠PBO\\ PC=PB\end{array}\right.$,
∴△CDP≌△POB(SAS).
点评 本题考查的是圆周角定理,菱形的判定,全等三角形的判定与性质,中位线的性质,解题的关键是SAS证明△CDP≌△POB.

练习册系列答案
相关题目
18.同一平面内,半径分别是2cm和3cm的两圆的圆心距为5cm,则这两圆的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
11.“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如表:
(1)小张如何进货,使进货款恰好为1300元?
(2)要使所获利润不超过进货价格的40%,则A型文具至少买多少只?
(3)在(2)的条件下,应如何选购文具使销售文具所获利润最大?最大利润是多少?
| 型号 | 进价(元/只) | 售价(元/只) |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
(2)要使所获利润不超过进货价格的40%,则A型文具至少买多少只?
(3)在(2)的条件下,应如何选购文具使销售文具所获利润最大?最大利润是多少?
15.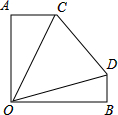 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
 如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )
如图,A在O的正北方向,B在O的正东方向,且OA=OB.某一时刻,甲车从A出发,以60km/h的速度朝正东方向行驶,与此同时,乙车从B出发,以40km/h的速度朝正北方向行驶.1小时后,位于点O处的观察员发现甲、乙两车之间的夹角为45°,即∠COD=45°,此时,甲、乙两人相距的距离为( )| A. | 90km | B. | 50$\sqrt{2}$km | C. | 20$\sqrt{13}$km | D. | 100km |
 如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).
如图,在矩形ABCD中,BC=10,AB=4,动点E从点B出发沿BC向终点C以每秒1个单位长度的速度运动,动点F沿折线BA-AD向终点D以每秒2个单位长度的速度运动,过点E作BF的平行线与过点F作BE的平行线相交于点G,若点E,F同时出发,当有一个点到达终点时,另一个点继续运动直至到达终点停止,四边形BEGF与矩形ABCD重叠部分的面积为S(平方单位),运动的时间为t(秒).