题目内容
10．
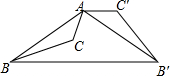如图，已知钝角三角形ABC，将△ABC绕点A按逆时针方向旋转110°得到△AB′C′，连接BB′，若AC′∥BB′，则∠CAB′的度数为（ ）| A． | 55° | B． | 65° | C． | 75° | D． | 85° |
分析 先根据旋转的性质得到∠BAB′=∠CAC′=110°，AB=AB′，根据等腰三角形的性质易得∠AB′B=35°，再根据平行线的性质得出∠C′AB′=∠AB′B=35°，然后利用∠CAB′=∠CAC′-∠C′AB′进行计算即可得出答案．
解答 解：∵将△ABC绕点A按逆时针方向旋转l10°得到△AB′C′，
∴∠BAB′=∠CAC′=110°，AB=AB′，
∴∠AB′B=$\frac{1}{2}$（180°-110°）=35°，
∵AC′∥BB′，
∴∠C′AB′=∠AB′B=35°，
∴∠CAB′=∠CAC′-∠C′AB′=110°-35°=75°．
故选C．
点评 此题考查了旋转的性质：掌握旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角是本题的关键．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
如图，在Rt△ABC中，∠B=90°，AC=60cm，∠A=60°，点D从点C出发沿CA方向以4cm/秒的速度向点A匀速运动，同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动．设点D、E运动的时间是t秒（0＜t≤15）．过点D作DF⊥BC于点F，连接DE，EF．
18．同一平面内，半径分别是2cm和3cm的两圆的圆心距为5cm，则这两圆的位置关系是（ ）
| A． | 相离 | B． | 相交 | C． | 外切 | D． | 内切 |
5．甲、乙两地之间的高速公路全长200千米，比原来国道的长度减少了20千米．高速公路通车后，某长途汽车的行驶速度提高了45千米/时，从甲地到乙地的行驶时间缩短了一半．设该长途汽车在原来国道上行驶的速度为x千米/时，根据题意，下列方程正确的是（ ）
| A． | $\frac{200}{x+45}$=$\frac{180}{x}$$•\frac{1}{2}$ | B． | $\frac{200}{x+45}$=$\frac{220}{x}$$•\frac{1}{2}$ | C． | $\frac{200}{x}$=$\frac{180}{x-45}$•$\frac{1}{2}$ | D． | $\frac{200}{x}$=$\frac{220}{x-45}$•$\frac{1}{2}$ |
15．
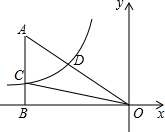如图，已知双曲线y=-$\frac{3}{x}$（x＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C，则△AOC的面积为（ ）
如图，已知双曲线y=-$\frac{3}{x}$（x＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C，则△AOC的面积为（ ）| A． | 6 | B． | $\frac{9}{2}$ | C． | 3 | D． | 2 |
2．4的算术平方根的相反数是（ ）
| A． | 2 | B． | -2 | C． | $\frac{1}{2}$ | D． | ±2 |
11．“六一”期间，小张购进100只两种型号的文具进行销售，其进价和售价之间的关系如表：
（1）小张如何进货，使进货款恰好为1300元？
（2）要使所获利润不超过进货价格的40%，则A型文具至少买多少只？
（3）在（2）的条件下，应如何选购文具使销售文具所获利润最大？最大利润是多少？
| 型号 | 进价（元/只） | 售价（元/只） |
| A型 | 10 | 12 |
| B型 | 15 | 23 |
（2）要使所获利润不超过进货价格的40%，则A型文具至少买多少只？
（3）在（2）的条件下，应如何选购文具使销售文具所获利润最大？最大利润是多少？