题目内容
15．正方形的面积是5，它的对角线长是（ ）| A． | $\sqrt{5}$ | B． | 2$\sqrt{5}$ | C． | $\sqrt{10}$ | D． | 2$\sqrt{10}$ |
分析 由正方形的对角线长为x，根据正方形的面积等于对角线积的一半即可列方程求出x的值．
解答 解：设正方形ABCD的对角线长为x，
则AC=BD=x，
∵S正方形ABCD=$\frac{1}{2}$AC•BD=$\frac{1}{2}$×x2=5，
解得：x=$\sqrt{10}$，
即这个正方形的对角线为 $\sqrt{10}$．
故选C．
点评 此题考查了正方形的性质，注意掌握正方形的面积等于对角线积的一半的性质是解此题的关键，难度一般．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
5．小张文具店每月一次性购进100件文具进行销售（能全部售出），有A，B两种文具可供选择，已知A型文具的进价是每件10元，B型文具的进价是每件15元，小张发现，所获总利润y（元）与A型文具的进货量x（件）之间存在着如下表所示的一次函数关系：
（1）求y与x之间的函数关系式，并写出自变量x的取值范围；
（2）在小张文具店中，B型文具的售价是23元；
（3）若在六月份，小张只有1300元，在进货量（100件）不变的前提下，六月份的最大利润是多少？
| 购进A型文具x件 | … | 10 | 20 | 30 | 40 | 50 | … |
| 总利润y元 | … | 740 | 680 | 620 | 560 | 500 | … |
（2）在小张文具店中，B型文具的售价是23元；
（3）若在六月份，小张只有1300元，在进货量（100件）不变的前提下，六月份的最大利润是多少？
6．
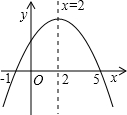已知函数y=ax2+bx+c 的图象如图所示，则下列判断不正确的是（ ）
已知函数y=ax2+bx+c 的图象如图所示，则下列判断不正确的是（ ）| A． | 关于x的方程ax2+bx+c=0的根是x1=-1，x2=5 | |
| B． | a-b+c＞0 | |
| C． | b=-4a | |
| D． | ac＜0 |
学习完轴对称后，黑板展示区出了一道作图题（不写作法，保留作图痕迹）．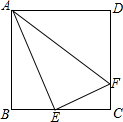
如图，正方形ABCD中，E是BC的中点，F是CD上的一点，且CD=4CF．求证：∠AEF=90°．
如图，把长方形纸片ABCD折叠，使其对角顶点C与A重合，折痕EF，若长方形的长BC为8，宽AB为4，则△AEF的面积为10．
5．
如图，用10块相同的长方形的地砖拼成一个长方形，则每块长方形地砖的面积为（ ）
如图，用10块相同的长方形的地砖拼成一个长方形，则每块长方形地砖的面积为（ ）| A． | 128 | B． | 256 | C． | 512 | D． | 1024 |