题目内容
6.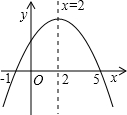 已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )
已知函数y=ax2+bx+c 的图象如图所示,则下列判断不正确的是( )| A. | 关于x的方程ax2+bx+c=0的根是x1=-1,x2=5 | |
| B. | a-b+c>0 | |
| C. | b=-4a | |
| D. | ac<0 |
分析 A、根据抛物线与x轴的交点坐标可得结论;
B、根据当x=-1时,y=0,代入解析式可得结论;
C、根据对称轴x=1,代入公式可得结论;
D、根据a、c的符号可得结论.
解答 解:A、由图象可知:抛物线与x轴的交点坐标为(-1,0)和(5,0),则关于x的方程ax2+bx+c=0的根是x1=-1,x2=5,所以此选项结论正确;
B、当x=-1时,y=0,即a-b+c=0,所以此选项判断不正确;
C、此抛物线的对称轴是:x=2,即-$\frac{b}{2a}$=2,b=-4a,所以此选项判断正确;
D、∵抛物线开口向下,
∴a<0,
∵抛物线与y轴交于正半轴,
∴c>0,
∴ac<0,所以此选项判断正确;
综上所述,本题判断不正确的是:B,
故选B.
点评 本题考查的是二次函数图象与系数的关系、抛物线与x轴的交点,掌握二次函数的性质、灵活运用数形结合思想是解题的关键,解答时,要熟练运用抛物线的对称性和抛物线上的点的坐标满足抛物线的解析式.

练习册系列答案
相关题目
14.下列计算中,正确的是( )
| A. | a3+a3=a6 | B. | a2•a5=a7 | C. | (2a)3=2a3 | D. | 3a8÷a2=3a4 |
15.正方形的面积是5,它的对角线长是( )
| A. | $\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | $\sqrt{10}$ | D. | 2$\sqrt{10}$ |
16.下列说法中错误的是( )
| A. | 368万精确到个位 | B. | 2.58精确到百分位 | ||
| C. | 5.7×102精确到十位 | D. | 566精确到个位 |
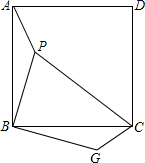 如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.
如图,已知P是正方形ABCD内一点,以点B为旋转中心,将△ABP按顺时针方向旋转使点A与点C重合,这时P点旋转到G点.