题目内容
9．二次函数$y=-\frac{1}{2}{（{x+3}）^2}-2$的顶点坐标是（ ）| A． | （3，2） | B． | （3，-2） | C． | （-3，-2） | D． | （-3，2） |
分析 确定此二次函数为抛物线，根据抛物线的性质，即可得出结论．
解答 解：∵二次函数$y=-\frac{1}{2}{（{x+3}）^2}-2$为抛物线解析式的顶点式，
∴抛物线的顶点为（-3，-2）．
故选C．
点评 本题考查了抛物线的性质，解题的关键是确定该二次函数为抛物线的顶点式．本题属于基础题型，难度不大，失分点在于（x+3）2顶点横坐标为-3．
练习册系列答案
相关题目
在△ABC中，AB=15，AC=20，∠B-∠C=90°，则线段BC的长度为7．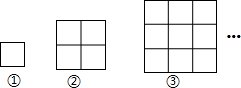
如图，每一幅图中均含有若干个正方形，第①个图形中含有1个正方形，第②个图形中含有5个正方形，按此规律下去，则第⑥个图象含有正方形的个数是（ ）
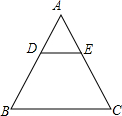如图，在△ABC中，在△ABC中，DE∥BC，若AD：AB=1：3，DE=2，则BC的长为6．